Problem Informations

• Problem Index: 1007
• Problem Link: Minimum Domino Rotations For Equal Row
• Topics: Array, Greedy

Problem Description

In a row of dominoes, tops[i] and bottoms[i] represent the top and bottom halves of the $i^{th}$ domino. (A domino is a tile with two numbers from 1 to 6 - one on each half of the tile.)

We may rotate the $i^{th}$ domino, so that tops[i] and bottoms[i] swap values.

Return the minimum number of rotations so that all the values in tops are the same, or all the values in bottoms are the same.

If it cannot be done, return -1.

Example 1:

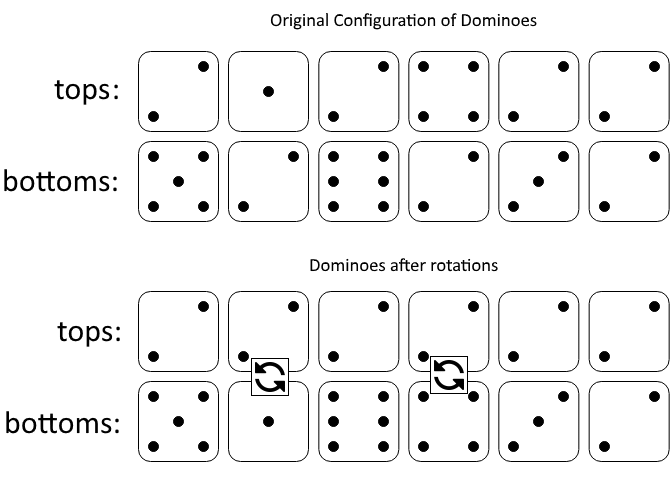
Input: tops = [2,1,2,4,2,2], bottoms = [5,2,6,2,3,2]
Output: 2
Explanation: 
The first figure represents the dominoes as given by tops and bottoms: before we do any rotations.
If we rotate the second and fourth dominoes, we can make every value in the top row equal to 2, as indicated by the second figure.

Example 2:

Input: tops = [3,5,1,2,3], bottoms = [3,6,3,3,4]
Output: -1
Explanation: 
In this case, it is not possible to rotate the dominoes to make one row of values equal.

Constraints:

• $2 \leq \text{tops.length} \leq 2 \times 10^4$
• $\text{bottoms.length} == \text{tops.length}$
• $1 \leq \text{tops}[i], \text{bottoms}[i] \leq 6$

Intuition

The problem can be visualized as arranging all dominos in a row such that either the top halves or the bottom halves of all dominos have the same number. We are allowed to rotate each domino individually as needed, swapping the numbers on its top and bottom halves. The main challenge is to determine the minimum number of such rotations required or to establish that it is impossible to make all numbers in a full row the same. However, given the constraint that each number is between 1 and 6, we can exploit this to efficiently find the solution by counting occurrences of each possible number.

Approach

The algorithm involves several key steps to determine the minimum number of rotations:

1. Count Occurrences: Initialize three vectors to track the frequency of each number (1 through 6) appearing on the top halves (topCount), bottom halves (bottomCount), and in total across both halves (totalCount) of the dominos.

2. Populate Frequency Counters: Iterate through each position in the dominos, updating the frequency counters:

   • Increment topCount for the number found on the top of the current domino.
   • Increment bottomCount for the number found on the bottom.
   • Increment totalCount for the number on the top. If the top and bottom numbers are different, also increment totalCount for the number on the bottom.

3. Check for Feasibility: Determine if it’s possible to have a full row of identical values. If no number appears a total of len times across both the top and bottom halves, it is impossible to make all values in a row equal, thus return -1.

4. Calculate Minimum Rotations: For numbers that could potentially fill an entire row (i.e., those whose total appearances match the length len of the dominos array), calculate the minimum rotations needed:

   • For each potential number, the number of rotations needed to create a uniform row is the total number of dominos minus the maximum appearances of the number in either the top or bottom halves.
   • Update the minimum rotation count accordingly.

5. Return the Result: If feasible numbers exist, the minimum rotation count will have a meaningful value, which will be returned as the result. Otherwise, it will have remained as INT_MAX and needs adjustment.

By breaking down the problem into counting and feasibility-checking steps, this approach efficiently determines whether and how the dominos can be rearranged to achieve the goal with minimal rotations. This method is both time-efficient and aligns well with the constraints of the problem.

Code

C++

class Solution {
public:
    int minDominoRotations(vector<int>& tops, vector<int>& bottoms) {
        int len = tops.size();
        int minRotations = INT_MAX;

        // Vectors to count appearances of each number (1 to 6) in top and bottom.
        vector<int> totalCount(6, 0), topCount(6, 0), bottomCount(6, 0);

        // Count the occurrences of each number in both tops and bottoms.
        for (int i = 0; i < len; i++) {
            topCount[tops[i] - 1]++;
            bottomCount[bottoms[i] - 1]++;
            totalCount[tops[i] - 1]++;
            if (tops[i] != bottoms[i]) {
                totalCount[bottoms[i] - 1]++;
            }
        }

        // If no number can fill a whole row, return -1.
        if (*max_element(totalCount.begin(), totalCount.end()) < len) {
            return -1;
        }

        // Calculate the minimum number of rotations needed to make all values in a row the same.
        for (int i = 0; i < 6; i++) {
            if (totalCount[i] == len) {
                minRotations = min(minRotations, len - max(topCount[i], bottomCount[i]));
            }
        }

        return minRotations;
    }
};

Python

class Solution:
    def minDominoRotations(self, tops, bottoms):
        from sys import maxsize

        len_tops = len(tops)
        min_rotations = maxsize

        # Lists to count appearances of each number (1 to 6) in top and bottom.
        total_count = [0] * 6
        top_count = [0] * 6
        bottom_count = [0] * 6

        # Count the occurrences of each number in both tops and bottoms.
        for i in range(len_tops):
            top_count[tops[i] - 1] += 1
            bottom_count[bottoms[i] - 1] += 1
            total_count[tops[i] - 1] += 1
            if tops[i] != bottoms[i]:
                total_count[bottoms[i] - 1] += 1

        # If no number can fill a whole row, return -1.
        if max(total_count) < len_tops:
            return -1

        # Calculate the minimum number of rotations needed to make all values in a row the same.
        for i in range(6):
            if total_count[i] == len_tops:
                min_rotations = min(min_rotations, len_tops - max(top_count[i], bottom_count[i]))

        return min_rotations

Complexity

• Time complexity: The algorithm iterates through the arrays multiple times. The first loop runs in $O(n)$ time to count the occurrences of each number in the tops and bottoms arrays, where $n$ is the length of the tops (or bottoms) array. This is followed by a constant-time operation in max_element, which takes $O(1)$ because the size of totalCount is always 6. The final loop iterates over a constant-sized array (6 elements in the range from 1 to 6), thus taking $O(1)$ as well. Therefore, the overall time complexity is $O(n)$.

• Space complexity: The space complexity is $O(1)$ since the additional space used by the algorithm does not scale with the input size n. We utilize a fixed amount of extra space, namely three arrays (totalCount, topCount, bottomCount), each with 6 elements to store the counts, and a few integer variables. Thus, the space usage remains constant regardless of n.