Problem Informations

Problem Index: 1028
Problem Link: Recover a Tree From Preorder Traversal
Topics: String, Tree, Depth-First Search, Binary Tree

Problem Description

We run a preorder depth-first search (DFS) on the root of a binary tree.

At each node in this traversal, we output D dashes (where D is the depth of this node), then we output the value of this node. If the depth of a node is D, the depth of its immediate child is D + 1. The depth of the root node is 0.

If a node has only one child, that child is guaranteed to be the left child.

Given the output traversal of this traversal, recover the tree and return its root.

Example 1:

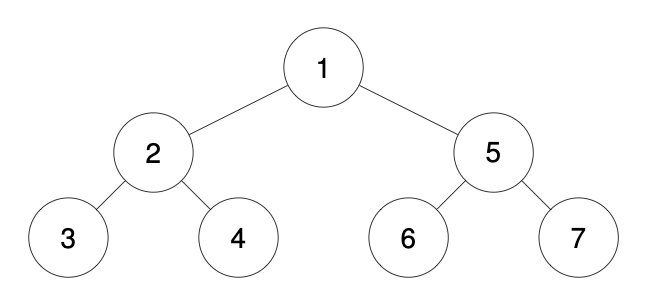
Example 1

Input: traversal = "1-2--3--4-5--6--7"
Output: [1,2,5,3,4,6,7]

Example 2:

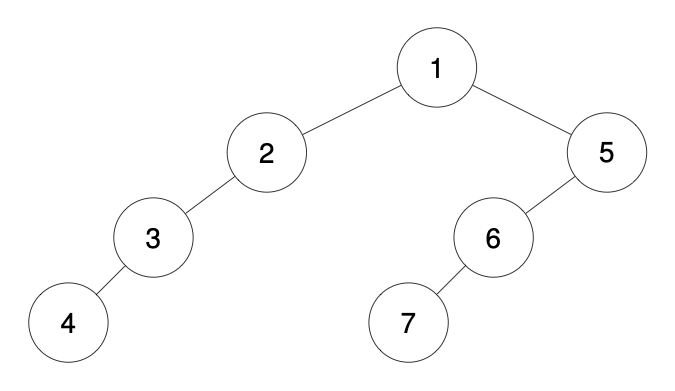
Example 2

Input: traversal = "1-2--3---4-5--6---7"
Output: [1,2,5,3,null,6,null,4,null,7]

Example 3:

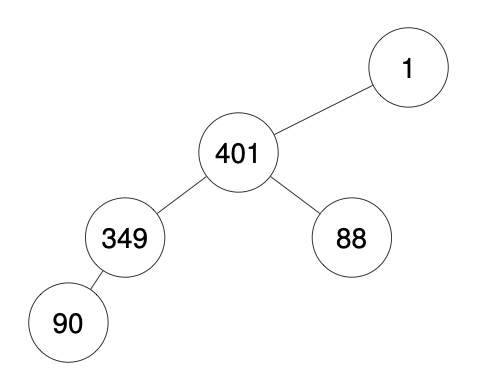
Example 3

Input: traversal = "1-401--349---90--88"
Output: [1,401,null,349,88,90]

Constraints:

The number of nodes in the original tree is in the range $[1, 1000]$.
$1 \leq \text{Node.val} \leq 10^9$

Intuition

To solve this tree recovery problem, the main task is to understand how depths and node values relate in the given traversal string. The input string is a result of a preorder depth-first search (DFS) traversal on the original binary tree. Each node is represented by a number prefixed by a certain number of dashes that indicate the depth of that node. By interpreting these prefixes accurately, we can reconstruct the binary tree structure. The challenge lies in using these dashes to manage tree depth while ensuring nodes are inserted in the correct positions.

Approach

The algorithm leverages a stack to manage the process of constructing the binary tree based on the preorder traversal details provided in the input string. Here’s a step-by-step breakdown of the approach:

Initialization and Root Node Creation:
- First, identify where the first dash (-) appears in the string. If there are no dashes, the string represents a single-node tree, and we can create and return a single TreeNode from the string.
- If dashes are present, extract the number up to the first dash to create the root node of the tree. Initialize a stack and push this root node onto the stack.
Iteration with Depth Calculation:
- Iterate over the traversal string starting from the first dash. For each segment of the string, calculate the depth of the current node by counting consecutive dashes.
- Use the depth to correlate with the stack size; the nodes corresponding to lesser or equal depths should be the ancestors of the current node. Nodes on the stack with depths greater than the current depth should be popped.
Node Value Extraction and Tree Construction:
- After determining the depth, extract the node’s value from the string. If there are no subsequent dashes marking the end of this node, it indicates this node is the last in the string.
- Check if the current node should be placed as a left or right child of the stack’s top node. Assign the current node as the left child if no left child is present; otherwise, assign it as the right child.
- Push the current node onto the stack, registering it as now the most recent ‘parent’ node ready to receive coming nodes as its children, if they have the appropriate depth.
Completion:
- Once the entire string is processed, the stack allows maintaining the relationship between nodes from different depths efficiently. The root node on the stack represents the recovered tree’s root.
- Return this root node representing the fully reconstructed binary tree.

This approach carefully maps the linear representation of the traversal back into a hierarchical tree structure by managing node depth effectively through stack operations. Each step ensures that the stack appropriately reflects the current layer of the tree during construction, adhering to the rules derived from preorder traversal and depth indications.

Code

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* recoverFromPreorder(string traversal) {
        // Find the position of the first dash, which indicates depth
        auto firstDashIdx = traversal.find('-');

        // If there's no dash, it's a single node tree
        if (firstDashIdx == string::npos) 
            return new TreeNode(stoi(traversal));

        // Create root node using the substring up to the first dash
        TreeNode* root = new TreeNode(stoi(traversal.substr(0, firstDashIdx)));

        // Use a stack to keep track of the tree nodes at each depth
        stack<TreeNode*> treeStack;
        treeStack.push(root);

        // Iterate through the rest of the traversal string
        for (int i = firstDashIdx; i < traversal.size(); i++) {
            int depthCount = 0;

            // Count consecutive dashes to determine depth
            while (i < traversal.size() && traversal[i] == '-') {
                depthCount++;
                i++;
            }

            // Pop nodes from the stack until the size matches the current depth
            while (treeStack.size() > depthCount) 
                treeStack.pop();

            // Find the next dash or end of string to get the current node's value
            auto nextDashIdx = traversal.find('-', i);
            TreeNode* currentNode;

            if (nextDashIdx == string::npos) {
                // If no more dashes, it's the last node in the path
                currentNode = new TreeNode(stoi(traversal.substr(i)));
                i = traversal.size(); // Move to the end of the string
            } else {
                // Extract the node value between current position and next dash
                currentNode = new TreeNode(stoi(traversal.substr(i, nextDashIdx - i)));
                i = nextDashIdx - 1; // Update the index to just before the next dash
            }

            // Check if the current node should be a left or right child
            if (treeStack.top()->left == nullptr) {
                // If no left child, assign current node to the left
                treeStack.top()->left = currentNode;
            } else {
                // Otherwise, assign current node to the right
                treeStack.top()->right = currentNode;
            }

            // Push the current node onto the stack
            treeStack.push(currentNode);
        }

        // Return the root of the reconstructed binary tree
        return root;
    }
};

Python

# Definition for a binary tree node.
class TreeNode:
    def __init__(self, x, left=None, right=None):
        self.val = x
        self.left = left
        self.right = right

class Solution:
    def recoverFromPreorder(self, traversal: str) -> TreeNode:
        # Find the position of the first dash, which indicates depth
        firstDashIdx = traversal.find('-')

        # If there's no dash, it's a single node tree
        if firstDashIdx == -1:
            return TreeNode(int(traversal))

        # Create root node using the substring up to the first dash
        root = TreeNode(int(traversal[:firstDashIdx]))

        # Use a stack to keep track of the tree nodes at each depth
        treeStack = [root]

        # Iterate through the rest of the traversal string
        i = firstDashIdx
        while i < len(traversal):
            depthCount = 0

            # Count consecutive dashes to determine depth
            while i < len(traversal) and traversal[i] == '-':
                depthCount += 1
                i += 1

            # Pop nodes from the stack until the size matches the current depth
            while len(treeStack) > depthCount:
                treeStack.pop()

            # Find the next dash or end of string to get the current node's value
            nextDashIdx = traversal.find('-', i)
            if nextDashIdx == -1:
                # If no more dashes, it's the last node in the path
                currentNode = TreeNode(int(traversal[i:]))
                i = len(traversal)  # Move to the end of the string
            else:
                # Extract the node value between current position and next dash
                currentNode = TreeNode(int(traversal[i:nextDashIdx]))
                i = nextDashIdx - 1  # Update the index to just before the next dash

            # Check if the current node should be a left or right child
            if treeStack[-1].left is None:
                # If no left child, assign current node to the left
                treeStack[-1].left = currentNode
            else:
                # Otherwise, assign current node to the right
                treeStack[-1].right = currentNode

            # Push the current node onto the stack
            treeStack.append(currentNode)

        # Return the root of the reconstructed binary tree
        return root

Complexity

Time complexity: The algorithm processes each character of the input string exactly once in a linear fashion, with operations inside loops that are efficiently managed using a stack. Therefore, the time complexity is $O(n)$, where $n$ is the length of the input string traversal.
Space complexity: The space complexity is determined by the maximum size of the stack, which corresponds to the maximum depth of the tree. In the worst case, the depth of the tree is proportional to the number of nodes, making the space complexity $O(d)$, where $d$ is the depth of the tree. In the worst case, this could also be $O(n)$ when each node represents a level of depth in a completely unbalanced tree.

CS Note
中

Leetcode 1028. Recover a Tree From Preorder Traversal