Problem Informations

• Problem Index: 1123
• Problem Link: Lowest Common Ancestor of Deepest Leaves
• Topics: Hash Table, Tree, Depth-First Search, Breadth-First Search, Binary Tree

Problem Description

Given the root of a binary tree, return the lowest common ancestor of its deepest leaves.

Recall that:

• The node of a binary tree is a leaf if and only if it has no children
• The depth of the root of the tree is $0$. if the depth of a node is $d$, the depth of each of its children is $d + 1$.
• The lowest common ancestor of a set $S$ of nodes, is the node $A$ with the largest depth such that every node in $S$ is in the subtree with root $A$.

Example 1:

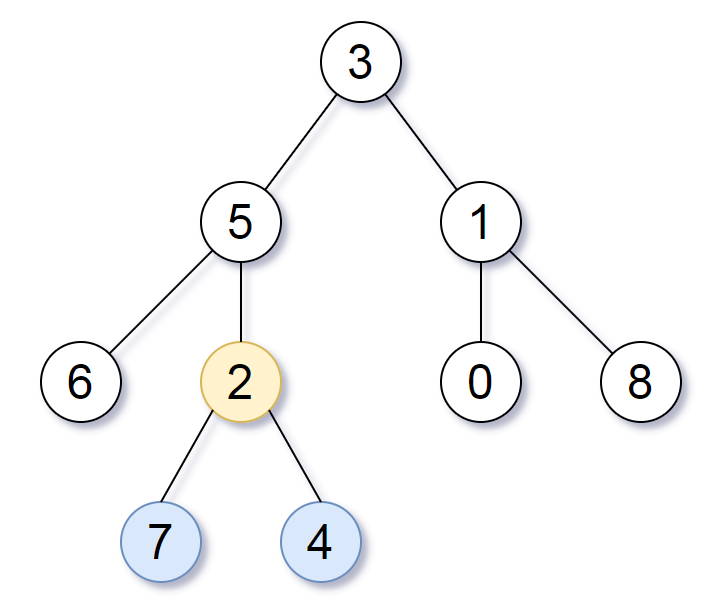
Input: root = [3,5,1,6,2,0,8,null,null,7,4]
Output: [2,7,4]
Explanation: We return the node with value 2, colored in yellow in the diagram.
The nodes coloured in blue are the deepest leaf-nodes of the tree.
Note that nodes 6, 0, and 8 are also leaf nodes, but the depth of them is 2, but the depth of nodes 7 and 4 is 3.

Example 2:

Input: root = [1]
Output: [1]
Explanation: The root is the deepest node in the tree, and it's the lca of itself.

Example 3:

Input: root = [0,1,3,null,2]
Output: [2]
Explanation: The deepest leaf node in the tree is 2, the lca of one node is itself.

Constraints:

• The number of nodes in the tree will be in the range $[1, 1000]$.
• $0 \leq \text{Node.val} < 1000$
• The values of the nodes in the tree are unique.

Note: This question is the same as 865: https://leetcode.com/problems/smallest-subtree-with-all-the-deepest-nodes/

Intuition

To solve the problem of finding the lowest common ancestor (LCA) of the deepest leaves in a binary tree, we need to understand two key points:

1. The deepest nodes are those at the maximum depth of the tree.
2. The LCA of a set of nodes is the deepest node from which all members of the set can be reached.

Given these requirements, a natural approach involves traversing the tree to measure the depth of every node and then determining the LCA for the deepest nodes.

Approach

The algorithm uses a recursive depth-first search (DFS) to traverse the tree and calculate the depth at each node. Here is a step-by-step explanation:

1. Base Case: If the current node is null, return a pair consisting of nullptr and depth 0. This indicates that we have reached the end of a path in the tree.

2. Recursive Case:

   • Perform DFS on the left child of the current node to get the deepest node and its depth in the left subtree.
   • Similarly, perform DFS on the right child to get the deepest node and its depth in the right subtree.

3. Analysis:

   • Compare the depths obtained from the left and right subtrees:
     • If the left subtree’s depth is greater, it indicates the deepest nodes reside in the left subtree. Thus, propagate the result from the left subtree and increment the depth by 1 to account for the current node.
     • If the right subtree’s depth is greater, it indicates the deepest nodes are in the right subtree. Similarly, propagate the result from the right subtree and increment the depth by 1.
     • If both subtrees have the same depth, it means the current node is the common ancestor for nodes deepest on either side. In this case, update the result to the current node and increment the depth.

4. Return Value: The function lcaDeepestLeaves initiates the DFS from the root node. The DFS function returns a pair where the first element is the LCA of the deepest leaves, and the second element is irrelevant to the output. The main function returns only the LCA node.

This approach ensures that, upon completion, we have identified the lowest common ancestor of the deepest nodes in the binary tree.

Code

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */

class Solution {
public:
    // Helper function to perform a depth-first search on the tree
    pair<TreeNode*, int> dfs(TreeNode* node) {
        if (node == nullptr) {
            // If the current node is null, return {nullptr, 0}
            return {nullptr, 0};
        }

        // Recursive DFS on the left and right subtrees
        pair<TreeNode*, int> leftResult = dfs(node->left);
        pair<TreeNode*, int> rightResult = dfs(node->right);

        // Compare the depths of the left and right subtree results
        if (leftResult.second > rightResult.second) {
            // If left subtree is deeper, propagate left result with incremented depth
            return {leftResult.first, leftResult.second + 1};
        } else if (leftResult.second < rightResult.second) {
            // If right subtree is deeper, propagate right result with incremented depth
            return {rightResult.first, rightResult.second + 1};
        } else {
            // If both have the same depth, the current node is the common ancestor
            return {node, leftResult.second + 1};
        }
    }

    // Function to find the lowest common ancestor of the deepest leaves
    TreeNode* lcaDeepestLeaves(TreeNode* root) {
        // The result's first item is the LCA of the deepest leaves
        return dfs(root).first;
    }
};

Python

# Definition for a binary tree node.
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class Solution:
    # Helper function to perform a depth-first search on the tree
    def dfs(self, node):
        if node is None:
            # If the current node is null, return (None, 0)
            return (None, 0)
        
        # Recursive DFS on the left and right subtrees
        leftResult = self.dfs(node.left)
        rightResult = self.dfs(node.right)
        
        # Compare the depths of the left and right subtree results
        if leftResult[1] > rightResult[1]:
            # If left subtree is deeper, propagate left result with incremented depth
            return (leftResult[0], leftResult[1] + 1)
        elif leftResult[1] < rightResult[1]:
            # If right subtree is deeper, propagate right result with incremented depth
            return (rightResult[0], rightResult[1] + 1)
        else:
            # If both have the same depth, the current node is the common ancestor
            return (node, leftResult[1] + 1)

    # Function to find the lowest common ancestor of the deepest leaves
    def lcaDeepestLeaves(self, root):
        # The result's first item is the LCA of the deepest leaves
        return self.dfs(root)[0]

Complexity

• Time complexity: $O(n)$

  The time complexity is $O(n)$ because each node of the binary tree is visited exactly once during the depth-first search (DFS). In the worst case, where the binary tree is a fully balanced binary tree, the DFS will traverse all nodes. Thus, the total time consumed is proportional to the number of nodes in the tree, which is denoted by $n$.

• Space complexity: $O(h)$

  The space complexity is $O(h)$, where $h$ is the height of the binary tree. This is due to the recursive nature of the DFS function. In the worst case, the space complexity is determined by the maximum depth of the function calls placed in the call stack, which corresponds to the height of the binary tree. For a balanced binary tree, the height $h$ is approximately $O(\log n)$, but in the worst-case scenario of a skewed binary tree, it becomes $O(n)$. Thus, in general, we consider the space complexity as $O(h)$.