Leetcode 1976. Number of Ways to Arrive at Destination

Jimmy   Mar 23, 2025   1565 words   ~40 mins
#Dynamic Programming #Graph #Topological Sort #Shortest Path

Table of Contents

Problem Informations

Problem Description

You are in a city that consists of $n$ intersections numbered from $0$ to $n - 1$ with bi-directional roads between some intersections. The inputs are generated such that you can reach any intersection from any other intersection and that there is at most one road between any two intersections.

You are given an integer $n$ and a 2D integer array $roads$ where $roads[i] = [u_i, v_i, time_i]$ means that there is a road between intersections $u_i$ and $v_i$ that takes $time_i$ minutes to travel. You want to know in how many ways you can travel from intersection $0$ to intersection $n - 1$ in the shortest amount of time.

Return the number of ways you can arrive at your destination in the shortest amount of time. Since the answer may be large, return it modulo $10^9 + 7$.

Example 1:

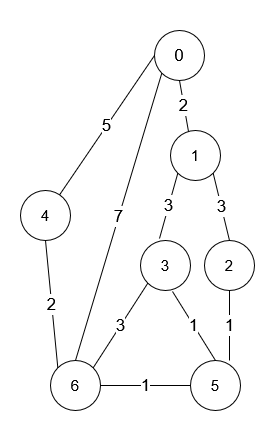
Example 1

Input: n = 7, roads = [[0,6,7],[0,1,2],[1,2,3],[1,3,3],[6,3,3],[3,5,1],[6,5,1],[2,5,1],[0,4,5],[4,6,2]]
Output: 4
Explanation: The shortest amount of time it takes to go from intersection 0 to intersection 6 is 7 minutes.
The four ways to get there in 7 minutes are:
- 0 ➝ 6
- 0 ➝ 4 ➝ 6
- 0 ➝ 1 ➝ 2 ➝ 5 ➝ 6
- 0 ➝ 1 ➝ 3 ➝ 5 ➝ 6

Example 2:

Input: n = 2, roads = [[1,0,10]]
Output: 1
Explanation: There is only one way to go from intersection 0 to intersection 1, and it takes 10 minutes.

Constraints:

  • $1 \leq n \leq 200$
  • $n - 1 \leq roads.length \leq \frac{n \cdot (n - 1)}{2}$
  • $roads[i].length == 3$
  • $0 \leq u_i, v_i \leq n - 1$
  • $1 \leq time_i \leq 10^9$
  • $u_i \neq v_i$
  • There is at most one road connecting any two intersections.
  • You can reach any intersection from any other intersection.

Intuition

The problem at hand is a graph traversal problem where we need to determine not only the shortest path from a starting node (intersection 0) to a destination node (intersection ( n-1 )) but also the number of distinct paths that achieve this shortest time. The primary intuition here is to employ graph traversal techniques to first find the shortest path distances from the start node to all other nodes and then to count the number of ways these shortest paths can be constructed.

Approach

The approach to solving this problem is divided into two main parts: computing the shortest paths and computing the number of distinct shortest paths.

  1. Graph Representation: The city and roads are represented using an adjacency list, where each node has a list of its neighboring nodes along with the time it takes to travel along those roads.

  2. Initialization:

    • We maintain a distance array (dp) that records the shortest distance from the starting intersection (node 0) to each node, initialized to infinity (LLONG_MAX) indicating that nodes are initially unreachable.
    • A separate array (ways) keeps track of the number of ways to reach each node using the shortest path, initialized to -1 indicating that the number of ways is yet to be computed.

  3. Find Shortest Paths:

    • We use a recursive function findShortestPaths to determine the shortest path from the start node (0) to every other node by updating the distance array dp.
    • We perform a depth-first traverse through the graph. If a shorter path is found to a node, its distance is updated, and the traverse continues recursively to its neighboring nodes.

  4. Compute Number of Ways:

    • A dynamic programming approach is utilized through the computeWays function to calculate the number of shortest paths arriving at the destination node (n-1).
    • Base Case: Directly at the starting node (0), there is one way to be yet use the shortest path, thus ways[0] is 1.
    • For each node, the function calculates the number of ways by aggregating paths from connected nodes if those nodes lie on a shortest path contributing to the current node’s shortest path (dp[neighbor.first] + neighbor.second == dp[index]).
    • The results are computed modulo (10^9 + 7) to handle large numbers as per the problem’s requirement.

  5. Final Computation:

    • We initiate the process by calling findShortestPaths starting from node 0.
    • After determining all shortest path distances, computeWays is called for the destination node n-1, which gives the number of distinct shortest paths from node 0 to node n-1.

By combining these steps, we calculate both the minimum time to reach the destination and the number of distinct ways to achieve that minimal time. This method effectively leverages depth-first search for shortest path determination and dynamic programming for path counting.

Code

C++

class Solution {
public:
    // Define constants
    static const long long MOD = 1e9 + 7;
    
    // Data members to store the number of ways, shortest paths, and adjacency list
    long long ans;
    vector<long long> dp;
    vector<long long> ways;
    vector<vector<pair<long long, long long>>> adjacencyList;

    // Function to find the shortest path from starting index to all other nodes
    void findShortestPaths(long long index, long long length) {
        // If the current path is shorter, update the shortest path
        if (dp[index] > length) {
            dp[index] = length;
            // Recursively find shortest paths for connected nodes
            for (const pair<long long, long long>& neighbor : adjacencyList[index]) {
                findShortestPaths(neighbor.first, length + neighbor.second);
            }
        }
    }

    // Function to calculate the number of ways to reach the destination in the shortest time
    long long computeWays(long long index) {
        // Base case: starting point
        if (index == 0) return 1;
        // Return precomputed ways if available
        if (ways[index] != -1) return ways[index];

        ways[index] = 0;
        // Analyze each connected node
        for (const pair<long long, long long>& neighbor : adjacencyList[index]) {
            // If the path is part of the shortest route, add ways from that node
            if (dp[neighbor.first] + neighbor.second == dp[index]) {
                ways[index] = (ways[index] + computeWays(neighbor.first)) % MOD;
            }
        }
        return ways[index];
    }

    // Main function to be called to count number of paths
    int countPaths(int n, vector<vector<int>>& roads) {
        // Initialize variables
        ans = 0;
        dp.clear();
        dp.resize(n, LLONG_MAX);
        ways.clear();
        ways.resize(n, -1);

        // Initialize the adjacency list
        adjacencyList.clear();
        adjacencyList.resize(n);

        // Populate adjacency list with data from roads
        for (const vector<int>& road : roads) {
            adjacencyList[road[0]].emplace_back(road[1], road[2]);
            adjacencyList[road[1]].emplace_back(road[0], road[2]);
        }

        // Find shortest paths from index 0
        findShortestPaths(0, 0);
        // Calculate ways to reach destination in shortest paths
        return computeWays(n - 1);
    }
};

Python

class Solution:
    # Define constants
    MOD = int(1e9 + 7)
    
    # Data members to store the number of ways, shortest paths, and adjacency list
    ans = 0
    dp = []
    ways = []
    adjacencyList = []

    # Function to find the shortest path from starting index to all other nodes
    def findShortestPaths(self, index, length):
        # If the current path is shorter, update the shortest path
        if self.dp[index] > length:
            self.dp[index] = length
            # Recursively find shortest paths for connected nodes
            for neighbor in self.adjacencyList[index]:
                self.findShortestPaths(neighbor[0], length + neighbor[1])

    # Function to calculate the number of ways to reach the destination in the shortest time
    def computeWays(self, index):
        # Base case: starting point
        if index == 0:
            return 1
        # Return precomputed ways if available
        if self.ways[index] != -1:
            return self.ways[index]

        self.ways[index] = 0
        # Analyze each connected node
        for neighbor in self.adjacencyList[index]:
            # If the path is part of the shortest route, add ways from that node
            if self.dp[neighbor[0]] + neighbor[1] == self.dp[index]:
                self.ways[index] = (self.ways[index] + self.computeWays(neighbor[0])) % self.MOD
        return self.ways[index]

    # Main function to be called to count number of paths
    def countPaths(self, n, roads):
        # Initialize variables
        self.ans = 0
        self.dp = [float('inf')] * n
        self.ways = [-1] * n

        # Initialize the adjacency list
        self.adjacencyList = [[] for _ in range(n)]

        # Populate adjacency list with data from roads
        for road in roads:
            self.adjacencyList[road[0]].append((road[1], road[2]))
            self.adjacencyList[road[1]].append((road[0], road[2]))

        # Find shortest paths from index 0
        self.findShortestPaths(0, 0)
        # Calculate ways to reach destination in shortest paths
        return self.computeWays(n - 1)

Complexity

  • Time complexity: The overall time complexity of this algorithm is $O(n^2)$, where $n$ is the number of intersections. The findShortestPaths function involves a recursive traversal of the graph, effectively implementing a depth-first search-like method over a connected graph, which takes $O(n^2)$ in the worst case due to the recursive exploration of each possible edge and update operation. Although the graph traversal and edge exploration might initially seem to be $O(E)$, the function essentially recalculates paths and comparisons iteratively, which leads to $O(n^2)$ considering $E \approx n^2$ in complete scenarios bounded by constraint limits. The computeWays function also runs in a similar traversal manner, involving potential paths checks but with an already established shortest path pattern to refine $O(n^2)$ operations. Therefore, both operations contribute to producing a resulting complexity proportional to $O(n^2)$, comprehensively covering both traversal and update operations within a bounded space.

  • Space complexity: The space complexity of this algorithm is $O(n + E)$, where $n$ is the number of intersections, and $E$ is the number of roads (edges). The primary data structures contributing to space usage are the vectors dp and ways, each occupying $O(n)$ space respectively for storing shortest path lengths and the number of ways to reach each intersection in the shortest time. Additionally, the adjacency list adjacencyList uses $O(E)$ space to store all the roads, represented as pairs in a list for each intersection node. Since the maximum $E$ can approach $O(n^2)$ with the mentioned constraints, the collective space requirement is bounded by the combined $O(n + E)$.

Disclaimer: All reference materials on this website are sourced from the internet and are intended for learning purposes only. If you believe any content infringes upon your rights, please contact me at csnote.cc@gmail.com, and I will remove the relevant content promptly.


Feedback Welcome: If you notice any errors or areas for improvement in the articles, I warmly welcome your feedback and corrections. Your input will help this blog provide better learning resources. This is an ongoing process of learning and improvement, and your suggestions are valuable to me. You can reach me at csnote.cc@gmail.com.