Problem Informations

Problem Index: 2467
Problem Link: Most Profitable Path in a Tree
Topics: Array, Tree, Depth-First Search, Breadth-First Search, Graph

Problem Description

There is an undirected tree with $n$ nodes labeled from $0$ to $n - 1$, rooted at node $0$. You are given a 2D integer array edges of length $n - 1$ where $edges[i] = [a_i, b_i]$ indicates that there is an edge between nodes $a_i$ and $b_i$ in the tree.

At every node $i$, there is a gate. You are also given an array of even integers amount, where amount[i] represents:

the price needed to open the gate at node $i$, if amount[i] is negative, or,
the cash reward obtained on opening the gate at node $i$, otherwise.

The game goes on as follows:

Initially, Alice is at node $0$ and Bob is at node bob.
At every second, Alice and Bob each move to an adjacent node. Alice moves towards some leaf node, while Bob moves towards node $0$.
For every node along their path, Alice and Bob either spend money to open the gate at that node, or accept the reward. Note that:
- If the gate is already open, no price will be required, nor will there be any cash reward.
- If Alice and Bob reach the node simultaneously, they share the price/reward for opening the gate there. In other words, if the price to open the gate is $c$, then both Alice and Bob pay $c / 2$ each. Similarly, if the reward at the gate is $c$, both of them receive $c / 2$ each.
If Alice reaches a leaf node, she stops moving. Similarly, if Bob reaches node $0$, he stops moving. Note that these events are independent of each other.

Return the maximum net income Alice can have if she travels towards the optimal leaf node.

Example 1:

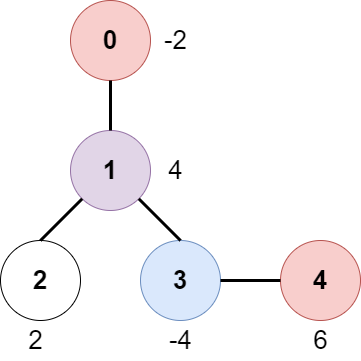
Example 1

Input: edges = [[0,1],[1,2],[1,3],[3,4]], bob = 3, amount = [-2,4,2,-4,6]
Output: 6
Explanation: 
The above diagram represents the given tree. The game goes as follows:
- Alice is initially on node 0, Bob on node 3. They open the gates of their respective nodes.
  Alice's net income is now -2.
- Both Alice and Bob move to node 1. 
  Since they reach here simultaneously, they open the gate together and share the reward.
  Alice's net income becomes -2 + (4 / 2) = 0.
- Alice moves on to node 3. Since Bob already opened its gate, Alice's income remains unchanged.
  Bob moves on to node 0, and stops moving.
- Alice moves on to node 4 and opens the gate there. Her net income becomes 0 + 6 = 6.
Now, neither Alice nor Bob can make any further moves, and the game ends.
It is not possible for Alice to get a higher net income.

Example 2:

Example 2

Input: edges = [[0,1]], bob = 1, amount = [-7280,2350]
Output: -7280
Explanation: 
Alice follows the path 0->1 whereas Bob follows the path 1->0.
Thus, Alice opens the gate at node 0 only. Hence, her net income is -7280.

Constraints:

$2 \leq n \leq 10^5$
edges.length == n - 1
edges[i].length == 2
$0 \leq a_i, b_i < n$
$a_i \neq b_i$
edges represents a valid tree.
$1 \leq bob < n$
amount.length == n
amount[i] is an even integer in the range $[-10^4, 10^4]$.

Intuition

The problem describes a scenario where Alice and Bob are navigating an undirected tree, starting from opposite ends (Alice from the root and Bob from a specific node), and their movements impact the net income Alice can gain. To effectively determine the optimal path for maximizing Alice’s net income, it’s crucial to understand that:

The tree structure allows for a natural traversal path using Depth-First Search (DFS).
Adjustment of the cost (or reward) at each node must account for both Alice’s and Bob’s movement and potential meeting points.
This necessitates identifying Bob’s path from his starting position to the root, as Alice’s income calculation is dependent on shared and isolated node influence.

Approach

The approach consists of several key steps:

Graph Representation and Initialization: We begin by representing the tree as an adjacency list using the given edge list. This data structure is efficient for graph traversal algorithms such as DFS.
Clear Node Connections: To aid in tree traversal without encountering cycles, the function clearNodeConnections modifies the adjacency list to prevent backtracking in DFS, essentially transforming the adjacency list into a Directed Acyclic Graph (DAG) rooted at node 0.
Determine Bob’s Path: The next step involves identifying Bob’s path back to the root (node 0). By doing so, we can accordingly adjust the amount array at each node Bob visits:
- For the first half of the path, nodes are marked with zero in the amount array since they are fully influenced by Bob.
- If the path length is odd, the node in the middle of Bob’s path will see its amount halved, reflecting the shared influence of both Bob and Alice at the same time.
Calculate Maximum Net Income for Alice: With the adjusted amount array, the function calculateMaxIncome performs a DFS to explore all possible paths from the root to any leaf. For each path, we accumulate Alice’s net income considering the modified amount values, and track the maximum income achieved.
Return the Result: Finally, the function returns the maximum net income Alice can achieve by following the best possible path calculated in the previous step.

The algorithm leverages a combination of DFS for path exploration and strategic modification of the node amount values based on Bob’s movements, thus effectively determining the optimal routes and adjustments for maximizing Alice’s net income.

Code

C++

class Solution {
public:
    // Helper function to clear visited nodes in the adjacency list
    void clearNodeConnections(vector<vector<int>>& adj, int node) {
        for (int child : adj[node]) {
            adj[child].erase(remove(adj[child].begin(), adj[child].end(), node), adj[child].end());
            clearNodeConnections(adj, child);
        }
    }

    // Recursive function to find Bob's path and modify the `amount` accordingly
    bool findBobPath(vector<vector<int>>& adj, int bob, vector<int>& amount, stack<int>& path, int node) {
        path.push(node);

        // If Bob's position is found
        if (node == bob) {
            bool isPathLengthOdd = (path.size() & 1);

            // Adjust amount for nodes in the path Bob has taken
            int halfPathSize = path.size() / 2;
            for (int i = 0; i < halfPathSize; i++) {
                amount[path.top()] = 0;
                path.pop();
            }

            // If path length is odd, share the amount at the middle node
            if (isPathLengthOdd) {
                amount[path.top()] /= 2;
            }

            return true;
        }

        // Traverse child nodes
        for (int child : adj[node]) {
            adj[child].erase(remove(adj[child].begin(), adj[child].end(), node), adj[child].end());
            // Recursively find Bob's path
            if (findBobPath(adj, bob, amount, path, child)) return true;
        }

        path.pop();  // Backtracking
        return false;
    }

    // Calculate the maximum possible net income Alice can have
    int calculateMaxIncome(vector<vector<int>>& adj, vector<int>& amount, int node, int currentValue) {
        currentValue += amount[node];

        // Leaf node check
        if (adj[node].empty()) {
            return currentValue;
        }

        int maxIncome = INT_MIN;

        // Traverse child nodes to find max income
        for (int child : adj[node]) {
            maxIncome = max(maxIncome, calculateMaxIncome(adj, amount, child, currentValue));
        }

        return maxIncome;
    }

    // Main function to determine the most profitable path for Alice
    int mostProfitablePath(vector<vector<int>>& edges, int bob, vector<int>& amount) {
        stack<int> path;
        vector<vector<int>> adj(amount.size());

        // Build adjacency list
        for (vector<int>& edge : edges) {
            adj[edge[0]].push_back(edge[1]);
            adj[edge[1]].push_back(edge[0]);
        }

        // Clear unnecessary node connections from adjacency list
        clearNodeConnections(adj, 0);

        // Find Bob's path and adjust the amounts accordingly
        findBobPath(adj, bob, amount, path, 0);

        // Calculate and return the maximum net income from Alice's optimal path
        return calculateMaxIncome(adj, amount, 0, 0);
    }
};

Python

class Solution:
    # Helper function to clear visited nodes in the adjacency list
    def clearNodeConnections(self, adj, node):
        for child in adj[node]:
            adj[child].remove(node)
            self.clearNodeConnections(adj, child)

    # Recursive function to find Bob's path and modify the `amount` accordingly
    def findBobPath(self, adj, bob, amount, path, node):
        path.append(node)

        # If Bob's position is found
        if node == bob:
            isPathLengthOdd = (len(path) & 1)

            # Adjust amount for nodes in the path Bob has taken
            halfPathSize = len(path) // 2
            for _ in range(halfPathSize):
                amount[path.pop()] = 0

            # If path length is odd, share the amount at the middle node
            if isPathLengthOdd:
                amount[path[-1]] //= 2

            return True

        # Traverse child nodes
        for child in adj[node]:
            adj[child].remove(node)
            # Recursively find Bob's path
            if self.findBobPath(adj, bob, amount, path, child):
                return True

        path.pop()  # Backtracking
        return False

    # Calculate the maximum possible net income Alice can have
    def calculateMaxIncome(self, adj, amount, node, currentValue):
        currentValue += amount[node]

        # Leaf node check
        if not adj[node]:
            return currentValue

        maxIncome = float('-inf')

        # Traverse child nodes to find max income
        for child in adj[node]:
            maxIncome = max(maxIncome, self.calculateMaxIncome(adj, amount, child, currentValue))

        return maxIncome

    # Main function to determine the most profitable path for Alice
    def mostProfitablePath(self, edges, bob, amount):
        path = []
        adj = [[] for _ in range(len(amount))]

        # Build adjacency list
        for edge in edges:
            adj[edge[0]].append(edge[1])
            adj[edge[1]].append(edge[0])

        # Clear unnecessary node connections from adjacency list
        self.clearNodeConnections(adj, 0)

        # Find Bob's path and adjust the amounts accordingly
        self.findBobPath(adj, bob, amount, path, 0)

        # Calculate and return the maximum net income from Alice's optimal path
        return self.calculateMaxIncome(adj, amount, 0, 0)

Complexity

Time complexity: The time complexity of the solution is $O(n)$. This is because each node is visited exactly once when constructing the adjacency list, clearing node connections, finding Bob’s path, and calculating the maximum possible net income for Alice, therefore providing a linear traversal in relation to the number of nodes $n$.
Space complexity: The space complexity of the solution is $O(n)$. This space encompasses the adjacency list representation of the tree and the stack used to keep track of the path for Bob. Both data structures require storage proportional to the number of nodes $n$.

CS Note
中

Leetcode 2467. Most Profitable Path in a Tree