Leetcode 2503. Maximum Number of Points From Grid Queries

Jimmy   Mar 28, 2025   1172 words   ~30 mins
#Array #Two Pointers #Breadth-First Search #Union Find #Sorting #Heap (Priority Queue) #Matrix

Table of Contents

Problem Informations

Problem Description

You are given an $m \times n$ integer matrix grid and an array queries of size $k$.

Find an array answer of size $k$ such that for each integer queries[i] you start in the top left cell of the matrix and repeat the following process:

  • If queries[i] is strictly greater than the value of the current cell that you are in, then you get one point if it is your first time visiting this cell, and you can move to any adjacent cell in all $4$ directions: up, down, left, and right.
  • Otherwise, you do not get any points, and you end this process.

After the process, answer[i] is the maximum number of points you can get. Note that for each query you are allowed to visit the same cell multiple times.

Return the resulting array answer.

Example 1:

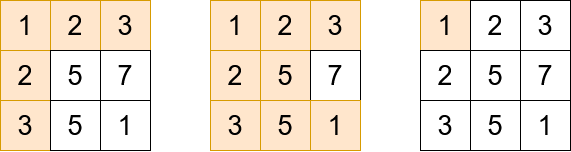
Example 1

Input: grid = [[1,2,3],[2,5,7],[3,5,1]], queries = [5,6,2]
Output: [5,8,1]
Explanation: The diagrams above show which cells we visit to get points for each query.

Example 2:

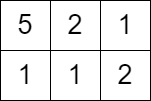
Example 2

Input: grid = [[5,2,1],[1,1,2]], queries = [3]
Output: [0]
Explanation: We can not get any points because the value of the top left cell is already greater than or equal to 3.

Constraints:

  • $m == \text{grid.length}$
  • $n == \text{grid}[i].\text{length}$
  • $2 \leq m, n \leq 1000$
  • $4 \leq m \times n \leq 10^{5}$
  • $k == \text{queries.length}$
  • $1 \leq k \leq 10^{4}$
  • $1 \leq \text{grid}[i][j], \text{queries}[i] \leq 10^{6}$

Intuition

The problem requires us to determine how many points we can accumulate when traversing from the top left cell of a grid, given a list of queries. The constraint is that for each cell visited, the query value must be greater than the cell’s value to gain a point. The goal is to find the maximum points attainable for each respective query through valid traversals.

The process resembles a search in the graph represented by the grid, where each cell is a node connected to its adjacent cells. Hence, a priority-based search algorithm suits the problem well to ensure we are efficiently checking cells in order of increasing value.

Approach

The algorithm employs a priority queue to facilitate traversals through the grid while evaluating each query. Here is a step-by-step breakdown:

  1. Initialization:

    • Create a priority_queue to store cells prioritized by their values (we use a negative sign to simulate a min-heap using C++’s max-heap).
    • Initialize visited to mark cells already visited.
    • Prepare a answerMemo vector initialized with a single zero to store precomputed results for optimization.

  2. Starting Point:

    • Insert the top-left cell (0, 0) of the grid into the priority_queue and mark it as visited.

  3. Process Each Query:

    • For each query, ensure that the answerMemo has entries at least as large as the query value. If not, extend answerMemo using values from the priority_queue.
    • For each value less than the current cell’s value, pop the cell from the priority_queue.
      • If the cell’s value is less than the query, increment the corresponding entry in answerMemo.
      • Check all four adjacent cells; if they have not been visited, mark them as visited, and push them into the priority_queue.

  4. Store Results:

    • Store the computed result either from the freshly calculated values or from answerMemo for each query into the answer vector.

  5. Finalize Output:

    • Return the answer vector containing the maximum points for each query.

This approach leverages the priority queue to dynamically compute the maximum traversable points using adjacency considerations, thereby providing efficient results for each query without recomputation.

Code

C++

class Solution {
public:
    vector<int> maxPoints(vector<vector<int>>& grid, vector<int>& queries) {
        vector<int> answerMemo(1, 0), answer;
        vector<vector<bool>> visited(grid.size(), vector<bool>(grid[0].size(), false));
        priority_queue<pair<int, pair<int, int>>> priorityQueue;
        int directions[] = {1, 0, -1, 0, 1};  // Directions for movement: right, down, left, up.
        int m = grid.size(), n = grid[0].size();
        
        // Initialize the starting point
        priorityQueue.push({-grid[0][0], {0, 0}});
        visited[0][0] = true;

        // Process each query
        for (int query : queries) {
            // If the query is not in the memo, extend the memo as needed
            if (query >= answerMemo.size()) {
                for (int i = answerMemo.size(); i <= query; i++) {
                    answerMemo.emplace_back(answerMemo.back());

                    // Process the priority queue
                    while (!priorityQueue.empty() && -priorityQueue.top().first < i) {
                        auto [val, pos] = priorityQueue.top();
                        auto [x, y] = pos;
                        priorityQueue.pop();
                        
                        // Increase the point count for current threshold
                        answerMemo[i]++;
                        
                        // Check all adjacent cells
                        for (int j = 0; j < 4; j++) {
                            int next_x = x + directions[j], next_y = y + directions[j + 1];
                            if (next_x < 0 || next_y < 0 || next_x >= m || next_y >= n || visited[next_x][next_y]) 
                                continue;
                            
                            visited[next_x][next_y] = true;
                            // Push the adjacent cell into the priority queue
                            priorityQueue.push({-grid[next_x][next_y], {next_x, next_y}});
                        }
                    }
                }
            }

            // Append the computed points to the answer based on query size
            if (query >= answerMemo.size())
                answer.emplace_back(answerMemo.back());
            else
                answer.emplace_back(answerMemo[query]);
        }
        
        return answer;
    }
};

Python

from heapq import heappush, heappop

class Solution:
    def maxPoints(self, grid, queries):
        answerMemo = [0]
        answer = []
        visited = [[False] * len(grid[0]) for _ in range(len(grid))]
        priorityQueue = []
        directions = [1, 0, -1, 0, 1]  # Directions for movement: right, down, left, up.
        m, n = len(grid), len(grid[0])

        # Initialize the starting point
        heappush(priorityQueue, (-grid[0][0], (0, 0)))
        visited[0][0] = True

        # Process each query
        for query in queries:
            # If the query is not in the memo, extend the memo as needed
            if query >= len(answerMemo):
                for i in range(len(answerMemo), query + 1):
                    answerMemo.append(answerMemo[-1])

                    # Process the priority queue
                    while priorityQueue and -priorityQueue[0][0] < i:
                        val, pos = heappop(priorityQueue)
                        x, y = pos

                        # Increase the point count for current threshold
                        answerMemo[i] += 1

                        # Check all adjacent cells
                        for j in range(4):
                            next_x, next_y = x + directions[j], y + directions[j + 1]
                            if next_x < 0 or next_y < 0 or next_x >= m or next_y >= n or visited[next_x][next_y]:
                                continue

                            visited[next_x][next_y] = True
                            # Push the adjacent cell into the priority queue
                            heappush(priorityQueue, (-grid[next_x][next_y], (next_x, next_y)))

            # Append the computed points to the answer based on query size
            if query >= len(answerMemo):
                answer.append(answerMemo[-1])
            else:
                answer.append(answerMemo[query])

        return answer

Complexity

  • Time complexity: The time complexity of this solution is $O(k \cdot \log(m \cdot n) + m \cdot n \cdot \log(m \cdot n))$. This complexity arises from two main processes: iterating through each query and processing the priority queue. For each query, there might be up to $m \cdot n$ cells to consider in the grid, which are pushed and popped from the priority queue. Each operation on the priority queue, including push and pop, takes $O(\log(m \cdot n))$ time. Given that there are $k$ queries, the total complexity is derived as such.

  • Space complexity: The space complexity is $O(m \cdot n + k)$. This space is required for storing the visited matrix, which tracks the visitation status of each cell in the $m \times n$ grid and the answerMemo array used to store results for each query value up to the maximum one in queries. The additional space for answer contributes to $O(k)$.

Disclaimer: All reference materials on this website are sourced from the internet and are intended for learning purposes only. If you believe any content infringes upon your rights, please contact me at csnote.cc@gmail.com, and I will remove the relevant content promptly.


Feedback Welcome: If you notice any errors or areas for improvement in the articles, I warmly welcome your feedback and corrections. Your input will help this blog provide better learning resources. This is an ongoing process of learning and improvement, and your suggestions are valuable to me. You can reach me at csnote.cc@gmail.com.