Problem Informations

• Problem Index: 2579
• Problem Link: Count Total Number of Colored Cells
• Topics: Math

Problem Description

There exists an infinitely large two-dimensional grid of uncolored unit cells. You are given a positive integer $n$, indicating that you must do the following routine for $n$ minutes:

• At the first minute, color any arbitrary unit cell blue.
• Every minute thereafter, color blue every uncolored cell that touches a blue cell.

Below is a pictorial representation of the state of the grid after minutes 1, 2, and 3.

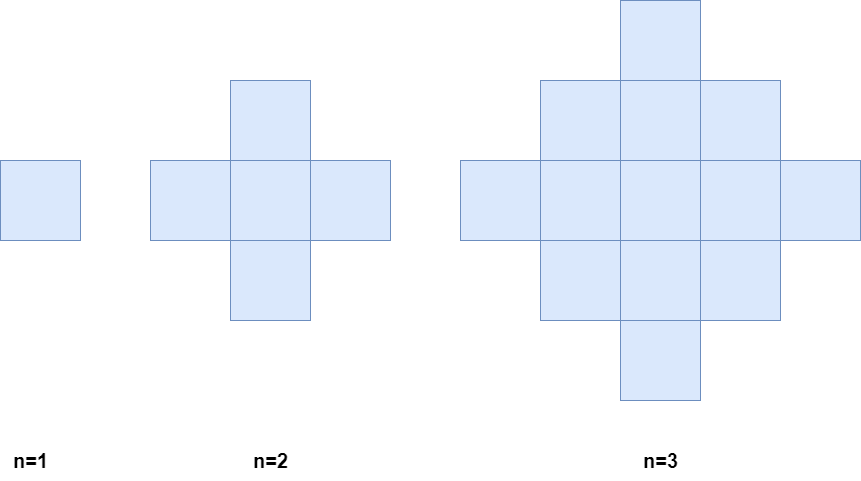
Return the number of colored cells at the end of $n$ minutes.

Example 1:

Input: n = 1
Output: 1
Explanation: After 1 minute, there is only 1 blue cell, so we return 1.

Example 2:

Input: n = 2
Output: 5
Explanation: After 2 minutes, there are 4 colored cells on the boundary and 1 in the center, so we return 5. 

Constraints:

• $1 \leq n \leq 10^5$

Intuition

The problem is about dynamically coloring a grid over a series of time steps. Initially, at the first minute, a single cell is colored and at each subsequent minute, every uncolored cell that is adjacent to a colored cell is also colored. The challenge is to determine the total number of colored cells after a specified number of minutes, $n$.

Upon analyzing the pattern of growth, it becomes clear that the newly colored cells form concentric layers around the initially colored cell. Consequently, the number of newly colored cells forms a pattern that is symmetrical and can be calculated mathematically rather than iteratively simulating the grid.

Approach

To solve this problem efficiently, we focus on deriving a formula based on observations of the grid pattern:

1. Initial Observation:

   • At minute 1, only the initial cell is colored, giving us a total of 1 colored cell.

2. Growth Pattern:

   • Starting from the second minute, the colored region grows outward, forming a diamond pattern around the central cell. This means, for each additional minute, new cells are colored in the four cardinal directions (up, down, left, right) and form the boundaries of an expanding diamond shape.
   • At minute 2, the original cell has 4 adjacent cells being colored, making the total 5 cells.
   • Extending this pattern, at each minute $k$, the additional boundary of cells form an increase by $4 \times (k - 1)$ cells.

3. General Formula:

   • By minute $n$, the number of additional cells colored is the sum of an arithmetic series: $4 \times \sum_{k=1}^{n-1} k = 2 \times n \times (n - 1)$.
   • Adding the initial cell, the total number of colored cells at minute $n$ is: $$\text{Total colored cells} = 2 \times n \times (n - 1) + 1$$

4. Conclusion:

   • This approach provides a direct computation for the number of colored cells after $n$ minutes without simulating the growth process on the grid, which is particularly efficacious given the constraint of $1 \leq n \leq 10^5$.

Code

C++

class Solution {
public:
    // This function calculates the number of colored cells after 'n' minutes
    long long coloredCells(int n) {
        // The formula 2 * n * (n - 1) + 1 calculates the total number of colored cells.
        // Here, 2 * n * (n - 1) counts the boundary cells colored over time,
        // and we add 1 for the initial central cell colored at the start.
        return static_cast<long long>(2) * n * (n - 1) + 1;
    }
};

Python

class Solution:
    # This function calculates the number of colored cells after 'n' minutes
    def coloredCells(self, n: int) -> int:
        # The formula 2 * n * (n - 1) + 1 calculates the total number of colored cells.
        # Here, 2 * n * (n - 1) counts the boundary cells colored over time,
        # and we add 1 for the initial central cell colored at the start.
        return 2 * n * (n - 1) + 1

Complexity

• Time complexity: $O(1)$

  The function computes the number of colored cells using a direct mathematical formula. It involves only a few basic arithmetic operations (multiplication and addition), each of which takes constant time. Hence, the overall time complexity is $O(1)$.

• Space complexity: $O(1)$

  The function uses a constant amount of space for storing the variables and performing the arithmetic operations. It does not require additional space that grows with the size of the input $n$. Therefore, the space complexity is $O(1)$.