Problem Informations

Problem Index: 2737
Problem Link: Find the Closest Marked Node
Topics: Array, Graph, Heap (Priority Queue), Shortest Path

Problem Description

You are given a positive integer $n$ which is the number of nodes of a 0-indexed directed weighted graph and a 0-indexed 2D array $edges$ where $edges[i] = [u_i, v_i, w_i]$ indicates that there is an edge from node $u_i$ to node $v_i$ with weight $w_i$.

You are also given a node $s$ and a node array $marked$; your task is to find the minimum distance from $s$ to any of the nodes in $marked$.

Return an integer denoting the minimum distance from $s$ to any node in $marked$ or $-1$ if there are no paths from $s$ to any of the marked nodes.

Example 1:

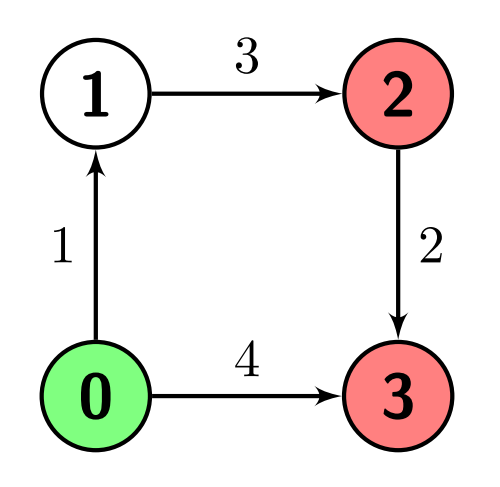
Input: $n = 4$, $edges = [[0,1,1],[1,2,3],[2,3,2],[0,3,4]]$, $s = 0$, $marked = [2,3]$
Output: $4$
Explanation: There is one path from node 0 (the green node) to node 2 (a red node), which is $0 \to 1 \to 2$, and has a distance of $1 + 3 = 4$.
There are two paths from node 0 to node 3 (a red node), which are $0 \to 1 \to 2 \to 3$ and $0 \to 3$, the first one has a distance of $1 + 3 + 2 = 6$ and the second one has a distance of $4$.
The minimum of them is $4$.

Example 2:

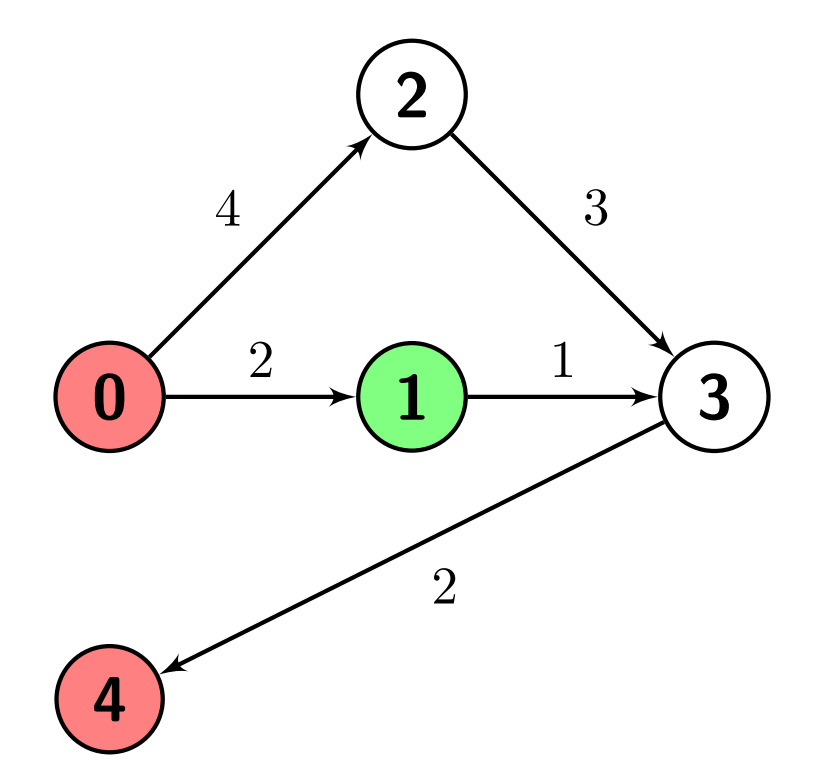
Input: $n = 5$, $edges = [[0,1,2],[0,2,4],[1,3,1],[2,3,3],[3,4,2]]$, $s = 1$, $marked = [0,4]$
Output: $3$
Explanation: There are no paths from node 1 (the green node) to node 0 (a red node).
There is one path from node 1 to node 4 (a red node), which is $1 \to 3 \to 4$, and has a distance of $1 + 2 = 3$.
So the answer is $3$.

Example 3:

Input: $n = 4$, $edges = [[0,1,1],[1,2,3],[2,3,2]]$, $s = 3$, $marked = [0,1]$
Output: $-1$
Explanation: There are no paths from node 3 (the green node) to any of the marked nodes (the red nodes), so the answer is $-1$.

Constraints:

$2 \leq n \leq 500$
$1 \leq \text{edges.length} \leq 10^4$
$\text{edges}[i].\text{length} = 3$
$0 \leq \text{edges}[i][0], \text{edges}[i][1] \leq n - 1$
$1 \leq \text{edges}[i][2] \leq 10^6$
$1 \leq \text{marked.length} \leq n - 1$
$0 \leq s, \text{marked}[i] \leq n - 1$
$s \neq \text{marked}[i]$
$\text{marked}[i] \neq \text{marked}[j]$ for every $i \neq j$
The graph might have repeated edges.
The graph is generated such that it has no self-loops.

Intuition

The problem involves finding the shortest path from a given node to any node in a set of marked nodes within a directed weighted graph. This is a classic application of the shortest path algorithms, often solved using Dijkstra’s algorithm when dealing with weighted edges and non-negative weights. The goal is to reach one of the marked nodes with the minimum possible path weight. If no such path exists, the function should return -1.

Approach

The approach involves the use of Dijkstra’s algorithm, which is efficient for finding the shortest path from one node to other nodes in a graph with non-negative edge weights. The algorithm utilizes a priority queue (min-heap) to always expand the least costly node. Here are the detailed steps implemented in the provided solution:

Graph Representation:
- Use an adjacency list to represent the graph. Each node points to a list of pairs, where each pair consists of a neighboring node and the weight of the edge connecting to it.
Initialization:
- Create a set of marked nodes for quick lookup.
- Use an array to keep track of visited nodes.
- Initialize a priority queue to facilitate Dijkstra’s algorithm. In this queue, nodes are stored as pairs where the first element is the negative distance (to simulate a min-heap) and the second element is the node itself.
Dijkstra’s Algorithm Setup:
- Begin by pushing the starting node into the priority queue with an initial distance of 0.
Priority Queue Processing:
- Continuously extract the node with the smallest distance. The node’s distance is inverted back to a positive number since we initially stored it as negative for priority queue purposes.
- If this node is one of the marked nodes, return its distance, as we have found the shortest path to a marked node.
- If the node has been visited already, skip further processing.
- Mark the node as visited.
- For each adjacent node, compute the distance through the current node and push these new distances and nodes into the priority queue for further exploration.
Termination:
- If the priority queue is exhausted without encountering a marked node, it indicates that no path exists from the start node to any of the marked nodes. Thus, the function returns -1.

This approach ensures that the shortest path to any marked node is found efficiently due to the priority queue’s ability to explore paths in order of increasing cost. The use of the adjacency list helps efficiently iterate over neighbors, and the marked nodes set allows quick verification if we reach any target node during graph traversal.

Code

C++

class Solution {
public:
    int minimumDistance(int n, vector<vector<int>>& edges, int startNode, vector<int>& markedNodes) {
        
        // Adjacency list to store the graph with weights.
        vector<vector<pair<int, int>>> adjacencyList(n);
        
        // Set to store marked nodes for quick lookup.
        set<int> markedSet;
        
        // Array to track visited nodes.
        vector<bool> visited(n, false);
        
        // Populate the adjacency list with edges.
        for (vector<int>& edge : edges) {
            adjacencyList[edge[0]].push_back({edge[1], edge[2]});
        }
        
        // Insert marked nodes into the marked set.
        for (int node : markedNodes) {
            markedSet.insert(node);
        }
        
        // Priority queue for Dijkstra's algorithm; storing pairs of (negative distance, node).
        priority_queue<pair<int, int>> pq;
        
        // Start the search from the startNode with an initial distance of 0.
        pq.push({0, startNode});
        
        while (!pq.empty()) {
            // Get the current node with the smallest distance.
            auto [currentLen, currentNode] = pq.top();
            pq.pop();
            
            // Check if the current node is marked; if so, return the distance.
            if (markedSet.count(currentNode) == 1) {
                return -currentLen;
            }
            
            // Skip if the node has already been visited.
            if (visited[currentNode]) {
                continue;
            }
            
            // Mark the current node as visited.
            visited[currentNode] = true;
            
            // Update distances for all adjacent nodes.
            for (pair<int, int> neighbor : adjacencyList[currentNode]) {
                // Add the adjacent node with updated distance to the priority queue.
                pq.push({currentLen - neighbor.second, neighbor.first});
            }
        }
        
        // If no path is found, return -1.
        return -1;
    }
};

Python

class Solution:
    def minimumDistance(self, n, edges, startNode, markedNodes):
        
        # Adjacency list to store the graph with weights.
        adjacencyList = [[] for _ in range(n)]
        
        # Set to store marked nodes for quick lookup.
        markedSet = set()
        
        # Array to track visited nodes.
        visited = [False] * n
        
        # Populate the adjacency list with edges.
        for edge in edges:
            adjacencyList[edge[0]].append((edge[1], edge[2]))
        
        # Insert marked nodes into the marked set.
        for node in markedNodes:
            markedSet.add(node)
        
        # Priority queue for Dijkstra's algorithm; storing pairs of (negative distance, node).
        pq = []
        
        # Start the search from the startNode with an initial distance of 0.
        heapq.heappush(pq, (0, startNode))
        
        while pq:
            # Get the current node with the smallest distance.
            currentLen, currentNode = heapq.heappop(pq)
            
            # Check if the current node is marked; if so, return the distance.
            if currentNode in markedSet:
                return -currentLen
            
            # Skip if the node has already been visited.
            if visited[currentNode]:
                continue
            
            # Mark the current node as visited.
            visited[currentNode] = True
            
            # Update distances for all adjacent nodes.
            for neighbor in adjacencyList[currentNode]:
                # Add the adjacent node with updated distance to the priority queue.
                heapq.heappush(pq, (currentLen - neighbor[1], neighbor[0]))
        
        # If no path is found, return -1.
        return -1

Complexity

Time complexity: The algorithm primarily uses Dijkstra’s shortest path algorithm with a priority queue. The time complexity of this implementation is $O((V + E) \log V)$, where $V$ is the number of vertices (or nodes) and $E$ is the number of edges. In this context, $V = n$, the number of nodes, and $E = \text{edges.length}$, the number of edges in the graph. For each vertex, we potentially process all of its edges and the priority queue operations take logarithmic time relative to the number of vertices.
Space complexity: The space complexity is $O(V + E)$, where $V$ is the number of vertices and $E$ is the number of edges. The adjacency list representation of the graph requires $O(V + E)$ space. Additionally, the priority queue may hold up to $O(V)$ elements in the worst case, and auxiliary data structures such as the visited array and markedSet will take $O(V)$ space as well.

CS Note
中

Leetcode 2737. Find the Closest Marked Node