Problem Informations

• Problem Index: 3068
• Problem Link: Find the Maximum Sum of Node Values
• Topics: Array, Dynamic Programming, Greedy, Bit Manipulation, Tree, Sorting

Problem Description

There exists an undirected tree with $n$ nodes numbered $0$ to $n - 1$. You are given a 0-indexed 2D integer array edges of length $n - 1$, where edges[i] = [u_i, v_i] indicates that there is an edge between nodes $u_i$ and $v_i$ in the tree. You are also given a positive integer $k$, and a 0-indexed array of non-negative integers nums of length $n$, where nums[i] represents the value of the node numbered $i$.

Alice wants the sum of values of tree nodes to be maximum, for which Alice can perform the following operation any number of times (including zero) on the tree:

• Choose any edge [u, v] connecting the nodes $u$ and $v$, and update their values as follows:
  • nums[u] = nums[u] XOR k
  • nums[v] = nums[v] XOR k

Return the maximum possible sum of the values Alice can achieve by performing the operation any number of times.

Example 1:

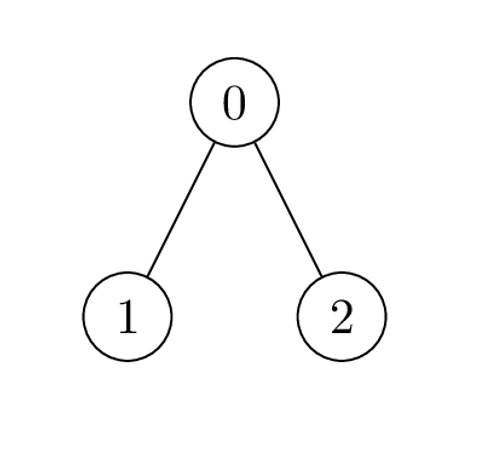
Input: nums = [1,2,1], k = 3, edges = [[0,1],[0,2]]
Output: 6
Explanation: Alice can achieve the maximum sum of 6 using a single operation:
- Choose the edge [0,2]. nums[0] and nums[2] become: 1 XOR 3 = 2, and the array nums becomes: [1,2,1] -> [2,2,2].
The total sum of values is 2 + 2 + 2 = 6.
It can be shown that 6 is the maximum achievable sum of values.

Example 2:

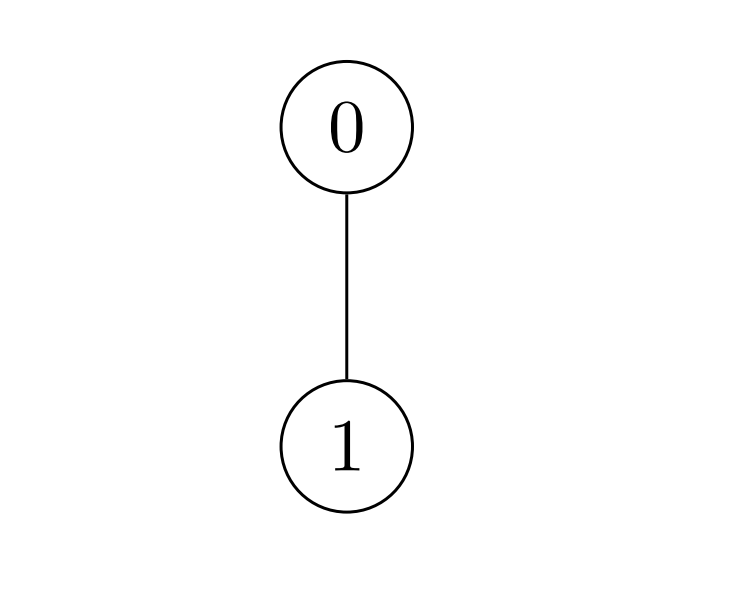
Input: nums = [2,3], k = 7, edges = [[0,1]]
Output: 9
Explanation: Alice can achieve the maximum sum of 9 using a single operation:
- Choose the edge [0,1]. nums[0] becomes: 2 XOR 7 = 5 and nums[1] become: 3 XOR 7 = 4, and the array nums becomes: [2,3] -> [5,4].
The total sum of values is 5 + 4 = 9.
It can be shown that 9 is the maximum achievable sum of values.

Example 3:

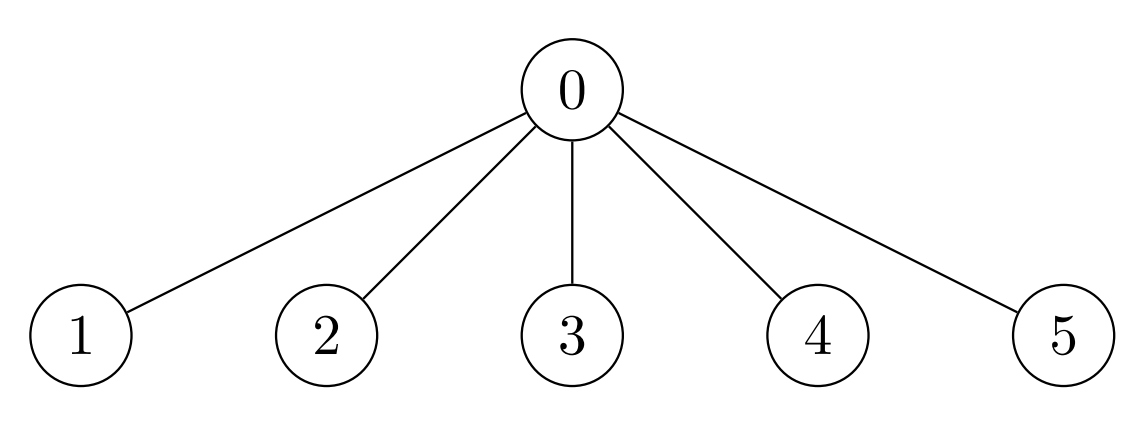
Input: nums = [7,7,7,7,7,7], k = 3, edges = [[0,1],[0,2],[0,3],[0,4],[0,5]]
Output: 42
Explanation: The maximum achievable sum is 42 which can be achieved by Alice performing no operations.

Constraints:

• $2 \leq n == \text{nums.length} \leq 2 \times 10^4$
• $1 \leq k \leq 10^9$
• $0 \leq \text{nums}[i] \leq 10^9$
• $\text{edges.length} == n - 1$
• $\text{edges}[i].length == 2$
• $0 \leq \text{edges}[i][0], \text{edges}[i][1] \leq n - 1$
• The input is generated such that edges represent a valid tree.

Intuition

The problem entails finding the maximum possible sum of node values in an undirected tree after performing any number of XOR-based operations. Each operation on an edge affects the values of the connected nodes. The inherent challenge is to decide which operations (if any) will maximize the sum of node values. The XOR operation toggles bits and may increase or decrease the node values. Hence, it is crucial to strategize which operations yield a beneficial outcome.

Approach

To maximize the sum of node values in the tree, we approach the problem with the following strategy:

1. Initial Calculations: We iterate over each node in the tree to determine both the original node value (originalValue) and the value after performing the XOR operation with k (flippedValue).

2. Maximize Node Contribution: For each node, we decide whether to use its original value or the value after XOR based on which one is larger. This choice directly contributes to the totalMaxSum, which is intended to capture the highest possible sum.

3. Track Minimum Flip Difference: While iterating, we also monitor the minFlipDifference, which represents the smallest absolute difference between a node’s original and flipped values. This difference is pivotal because it helps determine the optimum condition to adjust flips if needed.

4. Beneficial Flip Counting: For each node, we utilize an XOR operation to track flipCount, a measure of beneficial flips. A flip is considered beneficial if flippedValue exceeds originalValue. We XOR flipCount with the boolean result (flippedValue > originalValue), ensuring that flipCount represents an odd count when beneficial.

5. Final Adjustment: Post iteration, the totalMaxSum is adjusted by accounting for minFlipDifference and flipCount. If the count of beneficial operations is odd, we subtract the smallest possible difference, ensuring that an unnecessary suboptimal flip is mitigated.

The solution leverages the XOR operation characteristics to toggle node values beneficially across tree edges effectively. By maintaining a strategic overview of differences and counts, the algorithm ensures an optimal outcome without needing to explore every possible combination exhaustively.

Code

C++

class Solution {
public:
    // Function to return the minimum of two long long numbers.
    long long minValue(long long a, long long b) { 
        return (a < b) ? a : b; 
    }
    
    // Function to calculate the maximum possible sum of values by flipping edges.
    long long maximumValueSum(vector<int>& nums, int k, vector<vector<int>>& edges) {
        long long totalMaxSum = 0; // Variable to store the cumulative max sum of nodes.
        long long minFlipDifference = LLONG_MAX; // Tracks the smallest flip difference.
        long long flipCount = 0; // Counter to check the number of beneficial flips.
        long long numNodes = nums.size(); // Total number of nodes in the tree.
        
        for (int i = 0; i < numNodes; i++) {
            long long originalValue = nums[i]; // Original node value.
            long long flippedValue = nums[i] ^ k; // Node value after XOR with k.
            
            // Add the maximum of the original or flipped value to the total max sum.
            totalMaxSum += max(originalValue, flippedValue);
            
            // Update the minimum flip difference.
            minFlipDifference = minValue(minFlipDifference, abs(originalValue - flippedValue));
            
            // XOR-based flip counter to determine if the flip was beneficial.
            flipCount ^= flippedValue > originalValue;
        }
        
        // Adjust the total max sum based on the flip count and minimum flip difference.
        return totalMaxSum - minFlipDifference * flipCount;
    }
};

Python

class Solution:
    # Function to return the minimum of two long long numbers.
    def minValue(self, a, b):
        return a if a < b else b

    # Function to calculate the maximum possible sum of values by flipping edges.
    def maximumValueSum(self, nums, k, edges):
        totalMaxSum = 0  # Variable to store the cumulative max sum of nodes.
        minFlipDifference = float('inf')  # Tracks the smallest flip difference.
        flipCount = 0  # Counter to check the number of beneficial flips.
        numNodes = len(nums)  # Total number of nodes in the tree.
        
        for i in range(numNodes):
            originalValue = nums[i]  # Original node value.
            flippedValue = nums[i] ^ k  # Node value after XOR with k.
            
            # Add the maximum of the original or flipped value to the total max sum.
            totalMaxSum += max(originalValue, flippedValue)
            
            # Update the minimum flip difference.
            minFlipDifference = self.minValue(minFlipDifference, abs(originalValue - flippedValue))
            
            # XOR-based flip counter to determine if the flip was beneficial.
            flipCount ^= flippedValue > originalValue
        
        # Adjust the total max sum based on the flip count and minimum flip difference.
        return totalMaxSum - minFlipDifference * flipCount

Complexity

• Time complexity: $O(n)$

  The time complexity of the algorithm is $O(n)$, where $n$ is the number of nodes in the tree (which is also the length of the nums array). This is because the algorithm iterates through each node once to calculate potential maximum sums by considering both the original and XORed values. The operations inside the loop, including calculating XOR, determining maximum values, updating minimum flip difference, and updating the flip counter, all take constant time $O(1)$. Hence, iterating a single time through all nodes contributes to a linear time complexity.

• Space complexity: $O(1)$

  The space complexity of the algorithm is $O(1)$, which means it requires constant extra space regardless of the input size. The algorithm primarily uses a fixed number of variables: totalMaxSum, minFlipDifference, flipCount, and numNodes. These variables store intermediate computed values used during the calculation of the maximum sum and are not dependent on the input size. As a result, the space requirement does not scale with the size of the input, leading to a constant space complexity.