Problem Informations

• Problem Index: 3108
• Problem Link: Minimum Cost Walk in Weighted Graph
• Topics: Array, Bit Manipulation, Union Find, Graph

Problem Description

There is an undirected weighted graph with $n$ vertices labeled from $0$ to $n - 1$.

You are given the integer $n$ and an array edges, where edges[i] = [u_i, v_i, w_i] indicates that there is an edge between vertices $u_i$ and $v_i$ with a weight of $w_i$.

A walk on a graph is a sequence of vertices and edges. The walk starts and ends with a vertex, and each edge connects the vertex that comes before it and the vertex that comes after it. It’s important to note that a walk may visit the same edge or vertex more than once.

The cost of a walk starting at node $u$ and ending at node $v$ is defined as the bitwise AND of the weights of the edges traversed during the walk. In other words, if the sequence of edge weights encountered during the walk is $w_0, w_1, w_2, \ldots, w_k$, then the cost is calculated as $w_0$ & $w_1$ & $w_2$ & $\ldots$ & $w_k$, where & denotes the bitwise AND operator.

You are also given a 2D array query, where query[i] = [s_i, t_i]. For each query, you need to find the minimum cost of the walk starting at vertex $s_i$ and ending at vertex $t_i$. If there exists no such walk, the answer is $-1$.

Return the array answer, where answer[i] denotes the minimum cost of a walk for query $i$.

Example 1:

Input: n = 5, edges = [[0,1,7],[1,3,7],[1,2,1]], query = [[0,3],[3,4]]

Output: [1,-1]

Explanation:

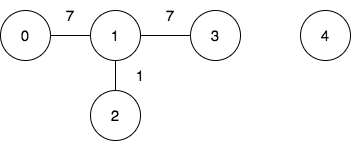
To achieve the cost of 1 in the first query, we need to move on the following edges: 0->1 (weight 7), 1->2 (weight 1), 2->1 (weight 1), 1->3 (weight 7).

In the second query, there is no walk between nodes 3 and 4, so the answer is -1.

Example 2:

Input: n = 3, edges = [[0,2,7],[0,1,15],[1,2,6],[1,2,1]], query = [[1,2]]

Output: [0]

Explanation:

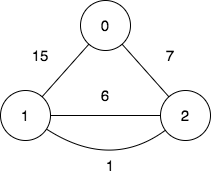
To achieve the cost of 0 in the first query, we need to move on the following edges: 1->2 (weight 1), 2->1 (weight 6), 1->2 (weight 1).

Constraints:

• $2 \leq n \leq 10^5$
• $0 \leq \text{edges.length} \leq 10^5$
• $\text{edges}[i].\text{length} == 3$
• $0 \leq u_i, v_i \leq n - 1$
• $u_i \neq v_i$
• $0 \leq w_i \leq 10^5$
• $1 \leq \text{query.length} \leq 10^5$
• $\text{query}[i].\text{length} == 2$
• $0 \leq s_i, t_i \leq n - 1$
• $s_i \neq t_i$

Intuition

The problem involves finding the minimum cost of a walk between two nodes in an undirected weighted graph with specific properties. A walk’s cost is determined by the bitwise AND of the weights of all edges traversed in that walk. Our goal is to create an efficient algorithm to determine this minimum cost for multiple node-pair queries.

The core intuition is to treat the graph as consisting of connected components. Each connected component can have a unique minimum weight derived from the AND operation of all the edge weights in that component. By leveraging depth-first search (DFS), we can explore these components, categorize them, and precompute this minimum weight for each component.

Approach

1. Graph Representation:

   • Utilize an adjacency list to represent the graph. The list stores each edge with its weight for both directions, as the graph is undirected.

2. Depth-First Search for Component Identification:

   • Use a depth-first search (DFS) to explore each node in the graph. Each node belongs to a connected component. Assign an index (i.e., group ID) to each component.
   • During the DFS, keep a running bitwise AND of all edge weights encountered. This operation computes the minimum possible cost for any walk entirely contained within the component.

3. Preprocessing:

   • Iterate over all nodes. If a node hasn’t been assigned a group, invoke the DFS starting from that node to classify all reachable nodes under a single group and compute the component’s minimum edge weight using the bitwise AND.

4. Handling Queries:

   • For each query, check the group ID of both nodes in the query.
   • If they belong to different components, it is impossible to complete a walk between them, hence return -1.
   • If they are part of the same component, return the precomputed minimum edge weight derived from the bitwise AND for that component.

This approach efficiently groups the graph’s nodes into components with minimal preprocessing. It ensures that each query can be answered in constant time by checking node membership in components, making the solution scalable to large input sizes.

Code

C++

class Solution {
public:
    // Helper function to assign group indices and determine the minimum edge weight
    // for each connected component.
    void set_group(int idx, int group_idx, vector<int>& group, vector<int>& group_val, vector<vector<pair<int, int>>>& edges_ll) {
        if (group[idx] != -1) return; // Node already assigned to a group
        group[idx] = group_idx; // Assign node to current group
        for (pair<int, int>& e : edges_ll[idx]) {
            // Update the minimum weight for the group
            group_val[group_idx] &= e.second;
            set_group(e.first, group_idx, group, group_val, edges_ll); // Continue depth-first search
        }
    }

    vector<int> minimumCost(int n, vector<vector<int>>& edges, vector<vector<int>>& query) {
        int group_idx = -1; // Initialize group index
        vector<int> group(n, -1); // Group index for each node, -1 means unvisited
        vector<int> group_val(n, INT_MAX); // Minimum edge weight for each group
        vector<vector<pair<int, int>>> edges_ll(n); // Adjacency list for edges
        vector<int> ans; // Storing results of queries

        // Build adjacency list
        for (vector<int>& e : edges) {
            edges_ll[e[0]].push_back({e[1], e[2]});
            edges_ll[e[1]].push_back({e[0], e[2]});
        }

        // Assign groups to connected components and calculate minimum edge weights
        for (int i = 0; i < n; i++) {
            if (group[i] != -1) continue; // Node already visited
            set_group(i, ++group_idx, group, group_val, edges_ll);
        }

        // Evaluate each query
        for (vector<int>& q : query) {
            if (group[q[0]] != group[q[1]]) {
                ans.push_back(-1); // Nodes are in different groups, no path exists
            } else {
                ans.push_back(group_val[group[q[0]]]); // Return minimum weight for the group
            }
        }

        return ans; // Return results for all queries
    }
};

Python

class Solution:
    # Helper function to assign group indices and determine the minimum edge weight
    # for each connected component.
    def set_group(self, idx, group_idx, group, group_val, edges_ll):
        if group[idx] != -1:
            return  # Node already assigned to a group
        group[idx] = group_idx  # Assign node to current group
        for e in edges_ll[idx]:
            # Update the minimum weight for the group
            group_val[group_idx] &= e[1]
            self.set_group(e[0], group_idx, group, group_val, edges_ll)  # Continue depth-first search

    def minimumCost(self, n, edges, query):
        group_idx = -1  # Initialize group index
        group = [-1] * n  # Group index for each node, -1 means unvisited
        group_val = [float('inf')] * n  # Minimum edge weight for each group
        edges_ll = [[] for _ in range(n)]  # Adjacency list for edges
        ans = []  # Storing results of queries

        # Build adjacency list
        for e in edges:
            edges_ll[e[0]].append((e[1], e[2]))
            edges_ll[e[1]].append((e[0], e[2]))

        # Assign groups to connected components and calculate minimum edge weights
        for i in range(n):
            if group[i] != -1:
                continue  # Node already visited
            self.set_group(i, group_idx + 1, group, group_val, edges_ll)
            group_idx += 1

        # Evaluate each query
        for q in query:
            if group[q[0]] != group[q[1]]:
                ans.append(-1)  # Nodes are in different groups, no path exists
            else:
                ans.append(group_val[group[q[0]]])  # Return minimum weight for the group

        return ans  # Return results for all queries

Complexity

• Time complexity: The time complexity of the given solution is $O(n + m)$, where $n$ is the number of vertices and $m$ is the number of edges present in the graph. This complexity arises because the algorithm visits each vertex and each edge exactly once. Constructing the adjacency list and assigning groups via the set_group function involves a depth-first search (DFS) that recursively traverses each vertex and its connected edges once.

• Space complexity: The space complexity is $O(n + m)$ as well. This space usage is due to the adjacency list representation of the graph, which requires storing $m$ edges, and the arrays group and group_val that store information for each of the $n$ vertices. The adjacency list itself uses $O(m)$ space, while the additional arrays use $O(n)$ space.