Problem Informations

• Problem Index: 311
• Problem Link: Sparse Matrix Multiplication
• Topics: Array, Hash Table, Matrix

Problem Description

Given two sparse matrices mat1 of size $m \times k$ and mat2 of size $k \times n$, return the result of $mat1 \times mat2$. You may assume that multiplication is always possible.

Example 1:

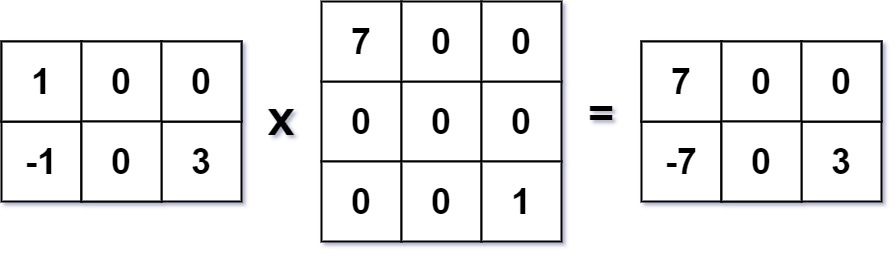
• Input: mat1 = [[1,0,0],[-1,0,3]], mat2 = [[7,0,0],[0,0,0],[0,0,1]]
• Output: [[7,0,0],[-7,0,3]]

Example 2:

• Input: mat1 = [[0]], mat2 = [[0]]
• Output: [[0]]

Constraints:

• $m == \text{mat1.length}$
• $k == \text{mat1[i].length} == \text{mat2.length}$
• $n == \text{mat2[i].length}$
• $1 \leq m, n, k \leq 100$
• $-100 \leq \text{mat1[i][j]}, \text{mat2[i][j]} \leq 100$

Intuition

When dealing with the multiplication of two sparse matrices, it is crucial to acknowledge that most of the elements involved are zeros and do not contribute to the final product. Therefore, by focusing on the non-zero elements, the computational effort can be significantly reduced. This insight guides us to an approach wherein we skip zero elements during the matrix multiplication process, ensuring that only necessary calculations are performed and reducing unnecessary iterations.

Approach

To effectively solve the problem of multiplying two sparse matrices, mat1 of size $m \times k$ and mat2 of size $k \times n$, we can leverage the sparsity by iterating only over non-zero elements. The procedure can be broken down into the following steps:

1. Result Initialization: Create a result matrix of size $m \times n$ initialized with zeros. This matrix will eventually store the product of mat1 and mat2.

2. Iterate Over mat1: Loop through each row i of mat1 and within each row, iterate over each column k.

3. Skip Zero Elements in mat1: If the element mat1[i][k] is zero, skip to the next column in mat1 as this element won’t contribute to the final product.

4. Iterate Over mat2: For each non-zero element mat1[i][k], iterate over each column j of mat2.

5. Skip Zero Elements in mat2: Similarly, if the element mat2[k][j] is zero, skip to the next column — as it similarly contributes nothing to the resulting matrix.

6. Compute and Accumulate Result: For non-zero elements, compute the product of mat1[i][k] and mat2[k][j] and add it to result[i][j]. This step directly accumulates only the necessary products for the resulting matrix.

7. Return the Result: After all relevant iterations, the result matrix will contain the computed product of mat1 and mat2, which can be returned as the final output.

This approach efficiently uses the sparse nature of the matrices, performing only essential operations, thereby making the matrix multiplication process more optimal than a naive calculation that might iteratively calculate unnecessary zero-based products.

Code

C++

class Solution {
public:
    // Function to multiply two sparse matrices mat1 and mat2
    vector<vector<int>> multiply(vector<vector<int>>& mat1, vector<vector<int>>& mat2) {
        int rowsMat1 = mat1.size();            // Number of rows in mat1
        int commonDim = mat1[0].size();        // Number of columns in mat1 or rows in mat2
        int colsMat2 = mat2[0].size();         // Number of columns in mat2
        
        // Initialize the result matrix with zeros
        vector<vector<int>> result(rowsMat1, vector<int>(colsMat2, 0));
        
        // Iterate through each element of mat1 by row and column
        for (int i = 0; i < rowsMat1; i++) {
            for (int k = 0; k < commonDim; k++) {
                // Skip zero elements in mat1 as they don't contribute to the result
                if (mat1[i][k] == 0) continue;
                
                // Iterate through each element of mat2 by column
                for (int j = 0; j < colsMat2; j++) {
                    // Skip zero elements in mat2 as they don't contribute to the result
                    if (mat2[k][j] == 0) continue;
                    
                    // Accumulate the product in the corresponding cell of the result matrix
                    result[i][j] += mat1[i][k] * mat2[k][j];
                }
            }
        }
        
        return result; // Return the resulting product matrix
    }
};

Python

class Solution:
    # Function to multiply two sparse matrices mat1 and mat2
    def multiply(self, mat1, mat2):
        rowsMat1 = len(mat1)            # Number of rows in mat1
        commonDim = len(mat1[0])        # Number of columns in mat1 or rows in mat2
        colsMat2 = len(mat2[0])         # Number of columns in mat2
        
        # Initialize the result matrix with zeros
        result = [[0 for _ in range(colsMat2)] for _ in range(rowsMat1)]
        
        # Iterate through each element of mat1 by row and column
        for i in range(rowsMat1):
            for k in range(commonDim):
                # Skip zero elements in mat1 as they don't contribute to the result
                if mat1[i][k] == 0:
                    continue
                
                # Iterate through each element of mat2 by column
                for j in range(colsMat2):
                    # Skip zero elements in mat2 as they don't contribute to the result
                    if mat2[k][j] == 0:
                        continue
                    
                    # Accumulate the product in the corresponding cell of the result matrix
                    result[i][j] += mat1[i][k] * mat2[k][j]
        
        return result  # Return the resulting product matrix

Complexity

• Time complexity: $O(m \times k \times n)$

  The time complexity of the algorithm is $O(m \times k \times n)$, where $m$ is the number of rows in mat1, $k$ is the number of columns in mat1 (or equivalently, the number of rows in mat2), and $n$ is the number of columns in mat2. This is because the algorithm iterates over each element of mat1 and for each non-zero element, iterates over the corresponding row in mat2. Despite the potential performance improvement due to the sparse nature of the matrices (as zero elements are skipped), the worst-case scenario still involves accessing each element, resulting in the time complexity mentioned.

• Space complexity: $O(m \times n)$

  The space complexity is $O(m \times n)$ because a result matrix of size $m \times n$ is initialized to store the product of mat1 and mat2. No additional data structures are used that significantly contribute to the space complexity, so the space required is determined solely by the size of the result matrix.