Problem Informations

Problem Index: 317
Problem Link: Shortest Distance from All Buildings
Topics: Array, Breadth-First Search, Matrix

Problem Description

You are given an $m \times n$ grid grid of values 0, 1, or 2, where:

each 0 marks an empty land that you can pass by freely,
each 1 marks a building that you cannot pass through, and
each 2 marks an obstacle that you cannot pass through.

You want to build a house on an empty land that reaches all buildings in the shortest total travel distance. You can only move up, down, left, and right.

Return the shortest travel distance for such a house. If it is not possible to build such a house according to the above rules, return -1.

The total travel distance is the sum of the distances between the houses of the friends and the meeting point.

Example 1: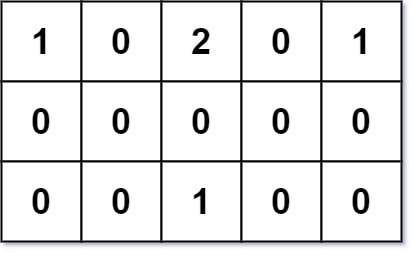
Example 1 Image

Input: grid = [[1,0,2,0,1],[0,0,0,0,0],[0,0,1,0,0]]
Output: 7
Explanation: Given three buildings at $(0,0)$, $(0,4)$, $(2,2)$, and an obstacle at $(0,2)$. The point $(1,2)$ is an ideal empty land to build a house, as the total travel distance of $3+3+1=7$ is minimal. So return 7.

Example 2:

Input: grid = [[1,0]]
Output: 1

Example 3:

Input: grid = [[1]]
Output: -1

Constraints:

$m == \text{grid.length}$
$n == \text{grid[i].length}$
$1 \le m, n \le 50$
grid[i][j] is either 0, 1, or 2.
There will be at least one building in the grid.

Intuition

The problem requires finding a suitable empty land on a grid, such that if a house is built there, the travel distance to all existing buildings is minimized. Given that movements are constrained up, down, left, and right, a breadth-first search (BFS) is a natural fit for exploring the shortest paths on a grid. Each building serves as a source for BFS to effectively compute the shortest distances to all other reachable points while accumulating these distances collaboratively from all buildings. The aim is to locate the empty land that not only is reachable from all buildings but also minimizes the total travel distance.

Approach

The approach consists of several steps. Let’s break down each part of the implemented algorithm:

Initialization:
- We begin by determining the grid’s size, m x n, and initializing various helper structures. Specifically, two 2D matrices, building_count and distance, are prepared to count how many buildings can reach each land and to accumulate the travel distance to each available cell, respectively.
- An array moves is used to facilitate directional movement during the BFS traversal.
Breadth-First Search (BFS) Traversal:
- Iterate over each cell in the grid to identify buildings (grid[i][j] == 1). For each building, initiate a BFS, which will explore all reachable lands and update the building_count and distance matrices appropriately.
- BFS uses a queue to track positions and the current cumulative distance. Each reachable adjacent land cell is marked, and the traversal state is updated incrementally for both distance and reachability.
- During traversal, ensure valid indices, unvisited status, and confirm that the destination cell is an empty land (grid[next_y][next_x] == 0). Each valid, reachable cell is updated in terms of cumulative distance and reachability.
Determine Optimal Land:
- With the BFS complete for all buildings, examine the building_count matrix to find empty lands (cells with grid[i][j] == 0) that are reachable from all buildings (building_count[i][j] == total_building_count).
- Track the minimum accumulated travel distance over these valid cells using a variable answer, ensuring to update only when a lower value is found.
Return Result:
- If any suitable land is found with minimized total travel distance, this value is returned. If no such land can feasibly reach all buildings, the function outputs -1, indicating impossibility under given constraints.

Through this systematic BFS from each building, the algorithm effectively calculates and compares path distances to potential house locations, ensuring the best possible choice is selected based on problem requirements.

Code

C++

class Solution {
public:
    int shortestDistance(vector<vector<int>>& grid) {
        int m = grid.size(); // Number of rows in the grid
        int n = grid[0].size(); // Number of columns in the grid
        int total_building_count = 0; // Total number of buildings in the grid

        // Directions to move in the grid: right, down, left, up
        int moves[] = {1, 0, -1, 0, 1}; 

        // To keep track of reachable buildings from each empty land cell
        vector<vector<int>> building_count(m, vector<int>(n, 0));
        // To accumulate distances from all buildings to each empty land cell
        vector<vector<int>> distance(m, vector<int>(n, 0));

        // Traverse the grid to find buildings and perform BFS from each building
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (grid[i][j] == 1) {
                    total_building_count++;

                    // Track visited cells during BFS
                    vector<vector<bool>> visited(m, vector<bool>(n, false));
                    // Use a queue for BFS; each element is a pair of coordinates and the current distance
                    queue<pair<pair<int, int>, int>> bfs;
                    bfs.push({{i, j}, 0});

                    while (!bfs.empty()) {
                        auto [pos, cur_dist] = bfs.front(); // Get front element of the queue
                        auto& [cur_y, cur_x] = pos; // Current coordinates
                        bfs.pop();

                        // Explore all 4 potential moves (right, down, left, up)
                        for (int k = 0; k < 4; k++) {
                            int next_y = cur_y + moves[k];
                            int next_x = cur_x + moves[k + 1];

                            // Check for valid coordinates, unvisited status, and passability as empty land
                            if (next_y < 0 || next_y >= m || next_x < 0 || next_x >= n || 
                                visited[next_y][next_x] || grid[next_y][next_x] != 0) {
                                continue;
                            }

                            // Mark this cell as visited
                            visited[next_y][next_x] = true;
                            // Increase the distance by one for this step
                            distance[next_y][next_x] += cur_dist + 1;
                            // Increase the reachable building count
                            building_count[next_y][next_x]++;
                            // Push the new position with updated distance into the queue
                            bfs.push({{next_y, next_x}, cur_dist + 1});
                        }
                    }
                }
            }
        }

        int answer = -1; // Variable to hold the minimum distance

        // Traverse the grid to find the optimal land for building the house
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                // Consider only empty lands that are reachable from all buildings
                if (grid[i][j] == 0 && building_count[i][j] == total_building_count) {
                    if (answer == -1 || answer > distance[i][j]) {
                        answer = distance[i][j]; // Update the shortest distance
                    }
                }
            }
        }

        return answer; // Return the shortest total travel distance
    }
};

Python

from collections import deque

class Solution:
    def shortestDistance(self, grid):
        m = len(grid)  # Number of rows in the grid
        n = len(grid[0])  # Number of columns in the grid
        total_building_count = 0  # Total number of buildings in the grid

        # Directions to move in the grid: right, down, left, up
        moves = [1, 0, -1, 0, 1]

        # To keep track of reachable buildings from each empty land cell
        building_count = [[0] * n for _ in range(m)]
        # To accumulate distances from all buildings to each empty land cell
        distance = [[0] * n for _ in range(m)]

        # Traverse the grid to find buildings and perform BFS from each building
        for i in range(m):
            for j in range(n):
                if grid[i][j] == 1:
                    total_building_count += 1
                    # Track visited cells during BFS
                    visited = [[False] * n for _ in range(m)]
                    # Use a queue for BFS; each element is a pair of coordinates and the current distance
                    bfs = deque()
                    bfs.append(((i, j), 0))

                    while bfs:
                        (cur_y, cur_x), cur_dist = bfs.popleft()

                        # Explore all 4 potential moves (right, down, left, up)
                        for k in range(4):
                            next_y = cur_y + moves[k]
                            next_x = cur_x + moves[k + 1]

                            # Check for valid coordinates, unvisited status, and passability as empty land
                            if (0 <= next_y < m and 0 <= next_x < n and
                                    not visited[next_y][next_x] and grid[next_y][next_x] == 0):
                                # Mark this cell as visited
                                visited[next_y][next_x] = True
                                # Increase the distance by one for this step
                                distance[next_y][next_x] += cur_dist + 1
                                # Increase the reachable building count
                                building_count[next_y][next_x] += 1
                                # Push the new position with updated distance into the queue
                                bfs.append(((next_y, next_x), cur_dist + 1))

        answer = -1  # Variable to hold the minimum distance

        # Traverse the grid to find the optimal land for building the house
        for i in range(m):
            for j in range(n):
                # Consider only empty lands that are reachable from all buildings
                if grid[i][j] == 0 and building_count[i][j] == total_building_count:
                    if answer == -1 or answer > distance[i][j]:
                        answer = distance[i][j]  # Update the shortest distance

        return answer  # Return the shortest total travel distance

Complexity

Time complexity: The time complexity of the solution is $O(m \times n \times k)$, where $m$ and $n$ are the dimensions of the grid, and $k$ is the number of buildings in the grid. For each building, a Breadth-First Search (BFS) is conducted over the grid, which takes $O(m \times n)$ time, leading to an overall complexity of $O(m \times n \times k)$.
Space complexity: The space complexity is $O(m \times n)$. This is due to the building_count, distance, and visited matrices, which occupy $O(m \times n)$ space each. The BFS queue can also grow to the size of $O(m \times n)$ in the worst-case scenario.

CS Note
中

Leetcode 317. Shortest Distance from All Buildings