Problem Informations

• Problem Index: 3208
• Problem Link: Alternating Groups II
• Topics: Array, Sliding Window

Problem Description

There is a circle of red and blue tiles. You are given an array of integers colors and an integer k. The color of tile i is represented by colors[i]:

• colors[i] == 0 means that tile i is red.
• colors[i] == 1 means that tile i is blue.

An alternating group is every k contiguous tiles in the circle with alternating colors (each tile in the group except the first and last one has a different color from its left and right tiles).

Return the number of alternating groups.

Note that since colors represents a circle, the first and the last tiles are considered to be next to each other.

Example 1:

Input: colors = [0,1,0,1,0], k = 3

Output: 3

Explanation:

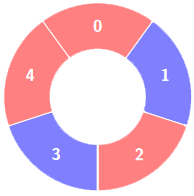
Alternating groups:

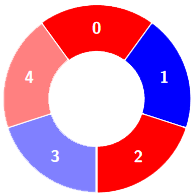
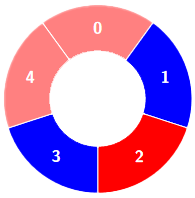
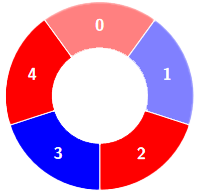
Example 2:

Input: colors = [0,1,0,0,1,0,1], k = 6

Output: 2

Explanation:

Alternating groups:

Example 3:

Input: colors = [1,1,0,1], k = 4

Output: 0

Explanation:

Constraints:

• $3 \leq \text{colors.length} \leq 10^5$
• $0 \leq \text{colors}[i] \leq 1$
• $3 \leq k \leq \text{colors.length}$

Intuition

The problem asks us to find all possible alternating groups of tiles within a circular arrangement. An alternating group consists of contiguous tiles where each tile alternates in color starting from a specified tile. Since the tiles form a circle, we need to account for groups that might wrap around the end of the array to the beginning.

To tackle this problem, the idea is to track sequences of alternating colors by scanning over the array while treating it as circular. This involves evaluating the colors of adjacent tiles and counting how many such sequences reach or exceed a given length, $k$.

The key obstacle is maintaining the circular property efficiently, and this can be achieved by virtually extending the array, using modular arithmetic to simulate the wrap-around effect.

Approach

The approach involves iterating through the tiles in a manner that treats the array as circular. This is done by iterating colors.length + k - 2 times. The additional $k - 2$ iterations ensure that all possible groups, including those that wrap around, are considered.

1. Initialization:

   • colorsLength is set to the length of the input colors array.
   • currentLength is initialized to 1, which keeps track of the length of the current alternating sequence being evaluated.
   • result is initialized to 0, which stores the count of valid alternating groups.

2. Iteration:

   • The loop runs from 0 to colorsLength + k - 2 to ensure that we check all possible starting positions, even those close to the end which might wrap to the beginning.
   • For each iteration at index i, we compare the color at the current index with the next color (using modulo arithmetic to account for the circular nature):
     • If the colors are the same, the alternating sequence is broken, and currentLength is reset to 1.
     • If they are different, it is considered a continuation of the sequence, and we increment currentLength.
   • If currentLength reaches $k$, this indicates a valid alternating group, so increment result.

3. Return:

   • Finally, return result, which represents the total number of alternating groups of at least length $k$.

This approach ensures each tile and potential starting point is checked exactly once, making the algorithm efficient with a time complexity of $O(n)$, where $n$ is the number of tiles. The approach effectively handles the circular property through modular arithmetic without needing to modify the initial array.

Code

C++

class Solution {
public:
    int numberOfAlternatingGroups(vector<int>& colors, int k) {
        int colorsLength = colors.size();
        int currentLength = 1; // Current alternating sequence length
        int result = 0; // Count of alternating groups

        // Iterate through the circular structure
        for (int i = 0; i < colorsLength + k - 2; i++) {
            // Compare current tile with the next in the circular array
            if (colors[i % colorsLength] == colors[(i + 1) % colorsLength]) {
                // Sequence broken, reset length
                currentLength = 1;
            } else {
                // Extend current sequence
                currentLength++;
            }

            // If the length of the current alternating sequence is at least k
            if (currentLength >= k) {
                result++;
            }
        }

        return result; // Return the total count of alternating groups
    }
};

Python

class Solution:
    def numberOfAlternatingGroups(self, colors, k):
        colorsLength = len(colors)
        currentLength = 1  # Current alternating sequence length
        result = 0  # Count of alternating groups

        # Iterate through the circular structure
        for i in range(colorsLength + k - 2):
            # Compare current tile with the next in the circular array
            if colors[i % colorsLength] == colors[(i + 1) % colorsLength]:
                # Sequence broken, reset length
                currentLength = 1
            else:
                # Extend current sequence
                currentLength += 1

            # If the length of the current alternating sequence is at least k
            if currentLength >= k:
                result += 1

        return result  # Return the total count of alternating groups

Complexity

• Time complexity: $O(n + k)$ where $n$ is the length of the colors array. Since the loop iterates through colorsLength + k - 2 elements, this results in an effective complexity of $O(n + k)$, which simplifies to $O(n)$ in terms of dominant factors when considering $n$ is the maximum.

• Space complexity: $O(1)$ which reflects the use of a fixed amount of extra space (for example, a few integer variables) regardless of the input size. The algorithm doesn’t require additional space proportional to the input size, thus constant space complexity.