Problem Informations

• Problem Index: 323
• Problem Link: Number of Connected Components in an Undirected Graph
• Topics: Depth-First Search, Breadth-First Search, Union Find, Graph

Problem Description

You have a graph of n nodes. You are given an integer n and an array edges where edges[i] = [a_i, b_i] indicates that there is an edge between a_i and b_i in the graph.

Return the number of connected components in the graph.

Example 1:

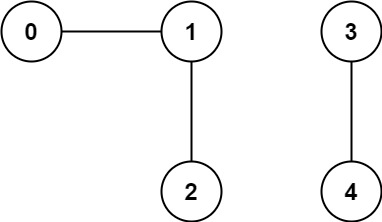
Input: n = 5, edges = [[0,1],[1,2],[3,4]]
Output: 2

Example 2:

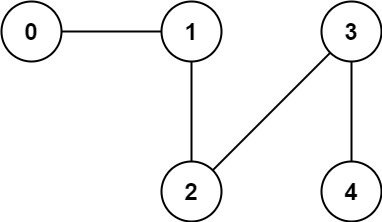
Input: n = 5, edges = [[0,1],[1,2],[2,3],[3,4]]
Output: 1

Constraints:

• $1 \leq n \leq 2000$
• $1 \leq \text{edges.length} \leq 5000$
• $\text{edges}[i].\text{length} == 2$
• $0 \leq a_i \leq b_i < n$
• $a_i \neq b_i$
• There are no repeated edges.

Intuition

The problem is to determine the number of connected components in an undirected graph with n nodes and a set of given edges. The graph can be decomposed into disjoint sets of nodes where each set represents a connected component. The primary challenge is to efficiently identify these sets. An effective approach is to use a Disjoint Set Union (DSU) data structure, which allows for efficient union and find operations, enabling us to track the connected components dynamically as we process each edge.

Approach

The solution involves utilizing a Disjoint Set Union (DSU) data structure, also known as Union-Find, to manage and discover connected components in the graph. Below are the detailed steps of the solution:

1. Initialize DSU: Start by initializing a vector dsu of size n, where each node is its own parent. This means initially, each node is considered a separate connected component.

2. Find Operation: Implement a findRoot function to determine the root representative of a node. This involves traversing up the parent chain until a node is its own parent. During this traversal, path compression is applied by pointing each node directly to the root, which optimizes future operations.

3. Union Operation: Create a uniteComponents function that connects two nodes, index1 and index2, by linking the root of one node to the root of the other. This operation effectively merges two disjoint sets into a single set if the nodes’ roots are different.

4. Union Edges: For each edge in the input, apply the uniteComponents function to join the nodes. This will recursively group nodes into connected components.

5. Count Components: To determine the number of connected components, iterate through each node and use the findRoot function to identify the root representative of each node. Collect these root representatives in a set, rootSet, which inherently stores unique elements.

6. Return Result: The size of the rootSet gives the total number of connected components in the graph, as each unique root represents a distinct connected component.

By following these steps, the algorithm efficiently identifies and counts the connected components in an undirected graph, leveraging the DSU structure for optimal performance in both the union and find operations.

Code

C++

class Solution {
private:
    vector<int> dsu;  // Disjoint set union (DSU) to track connected components

    // Find the root representative of the component for the given index.
    int findRoot(int index) {
        if (dsu[index] == index) {
            return index;  // The node is the root of itself
        } else {
            // Path compression by pointing node directly to the root
            return dsu[index] = findRoot(dsu[index]);
        }
    }

    // Union two nodes by connecting their components.
    void uniteComponents(int index1, int index2) {
        // Connect the roots of the components if they are different
        if (findRoot(index1) != findRoot(index2)) {
            dsu[findRoot(index2)] = findRoot(index1);
        }
    }

public:
    // Count the number of connected components in the graph
    int countComponents(int n, vector<vector<int>>& edges) {
        dsu.resize(n);  // Initialize DSU with each node as its own parent

        // Initially set each node to be its own parent
        for (int i = 0; i < n; i++) {
            dsu[i] = i;
        }

        // Union the nodes that are connected by edges
        for (vector<int>& edge : edges) {
            uniteComponents(edge[0], edge[1]);
        }

        // Set to keep track of the unique root representatives
        set<int> rootSet;
        for (int i = 0; i < n; i++) {
            rootSet.insert(findRoot(i));  // Find root for each node
        }

        // The size of the set gives the number of connected components
        return rootSet.size();
    }
};

Python

class Solution:
    def __init__(self):
        self.dsu = []  # Disjoint set union (DSU) to track connected components

    # Find the root representative of the component for the given index.
    def findRoot(self, index):
        if self.dsu[index] == index:
            return index  # The node is the root of itself
        else:
            # Path compression by pointing node directly to the root
            self.dsu[index] = self.findRoot(self.dsu[index])
            return self.dsu[index]

    # Union two nodes by connecting their components.
    def uniteComponents(self, index1, index2):
        # Connect the roots of the components if they are different
        root1 = self.findRoot(index1)
        root2 = self.findRoot(index2)
        if root1 != root2:
            self.dsu[root2] = root1

    # Count the number of connected components in the graph
    def countComponents(self, n, edges):
        self.dsu = list(range(n))  # Initialize DSU with each node as its own parent

        # Initially set each node to be its own parent
        for i in range(n):
            self.dsu[i] = i

        # Union the nodes that are connected by edges
        for edge in edges:
            self.uniteComponents(edge[0], edge[1])

        # Set to keep track of the unique root representatives
        rootSet = set()
        for i in range(n):
            rootSet.add(self.findRoot(i))  # Find root for each node

        # The size of the set gives the number of connected components
        return len(rootSet)

Complexity

• Time complexity: The time complexity is $O(n + m \cdot \alpha(n))$, where $n$ is the number of nodes and $m$ is the number of edges. The complexity arises as follows:

  • Initializing the DSU takes $O(n)$ time, as each node is set as its own parent.
  • For each edge, the uniteComponents function is invoked. The findRoot function called within uniteComponents has an amortized time complexity of $O(\alpha(n))$, where $\alpha$ is the inverse Ackermann function, which is very slow-growing and nearly constant for all practical purposes. Hence, processing all edges takes $O(m \cdot \alpha(n))$ time.
  • The final loop to find the root of each node requires $O(n \cdot \alpha(n))$ time, but it is dominated by the previous step, resulting in the overall time complexity being $O(n + m \cdot \alpha(n))$.

• Space complexity: The space complexity is $O(n)$.

  • The DSU array dsu has $n$ elements, corresponding to the $n$ nodes, leading to $O(n)$ space usage.
  • The additional space for the rootSet, which holds the unique root representatives, is negligible in terms of asymptotic complexity, as it can store at most $n$ elements, also resulting in $O(n)$ space.