Problem Informations

• Problem Index: 3394
• Problem Link: Check if Grid can be Cut into Sections
• Topics: Array, Sorting

Problem Description

You are given an integer n representing the dimensions of an $n \times n$ grid, with the origin at the bottom-left corner of the grid. You are also given a 2D array of coordinates rectangles, where rectangles[i] is in the form $[start_x, start_y, end_x, end_y]$, representing a rectangle on the grid. Each rectangle is defined as follows:

• $(start_x, start_y)$: The bottom-left corner of the rectangle.
• $(end_x, end_y)$: The top-right corner of the rectangle.

Note that the rectangles do not overlap. Your task is to determine if it is possible to make either two horizontal or two vertical cuts on the grid such that:

• Each of the three resulting sections formed by the cuts contains at least one rectangle.
• Every rectangle belongs to exactly one section.

Return true if such cuts can be made; otherwise, return false.

Example 1:

Input: n = 5, rectangles = [[1,0,5,2],[0,2,2,4],[3,2,5,3],[0,4,4,5]]

Output: true

Explanation:

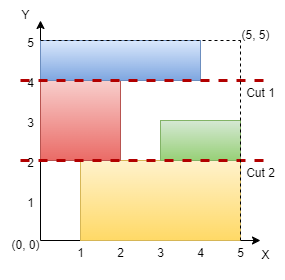
The grid is shown in the diagram. We can make horizontal cuts at y = 2 and y = 4. Hence, output is true.

Example 2:

Input: n = 4, rectangles = [[0,0,1,1],[2,0,3,4],[0,2,2,3],[3,0,4,3]]

Output: true

Explanation:

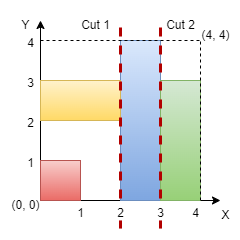
We can make vertical cuts at x = 2 and x = 3. Hence, output is true.

Example 3:

Input: n = 4, rectangles = [[0,2,2,4],[1,0,3,2],[2,2,3,4],[3,0,4,2],[3,2,4,4]]

Output: false

Explanation:

We cannot make two horizontal or two vertical cuts that satisfy the conditions. Hence, output is false.

Constraints:

• $3 \leq n \leq 10^9$
• $3 \leq \text{rectangles.length} \leq 10^5$
• $0 \leq \text{rectangles}[i][0] < \text{rectangles}[i][2] \leq n$
• $0 \leq \text{rectangles}[i][1] < \text{rectangles}[i][3] \leq n$
• No two rectangles overlap.

Intuition

The problem involves determining if we can partition a set of non-overlapping rectangles laid on an ( n \times n ) grid into three contiguous sections. The constraints are that either two horizontal or two vertical cuts must be made, and each section must contain at least one rectangle. A rectangle should not span across two sections. Given these conditions, a natural approach is to examine potential horizontal and vertical lines that could serve as cuts and check their validity based on the criteria outlined.

Approach

The solution utilizes a sweeping line technique, whereby we analyze potential cutting lines based on the boundaries of the rectangles. We are interested in identifying positions where we can place the cuts such that they cleanly separate the rectangles into three or more sections.

1. Extract Critical Points: We begin by identifying critical x and y coordinates, which represent the horizontal and vertical edges of the rectangles. For each rectangle, we consider starting and ending coordinates to determine potential cuts. We also keep track of the maximum x and y coordinates to ensure we do not attempt to cut beyond the grid’s boundaries.

2. Store and Sort Edges: Once we’ve identified the critical points, we store these in two separate lists for horizontal and vertical edges. We use negative values to signify the end of a rectangle’s boundary. Sorting these lists by the absolute coordinate values allows us to traverse from the least to the greatest, ensuring we consider potential cut lines appropriately.

3. Determine Valid Cuts:

   • We traverse through the sorted lists, maintaining an active block counter to determine whether a line is currently crossing any rectangle.
   • A horizontal or vertical segment is deemed a valid cut if:
     • The active block counter returns to zero, signifying a potential cut between rectangles.
     • The cut is not at the maximum x or y boundary.
   • If two such cuts are identified in either the horizontal or vertical traversal, we immediately return true, indicating a valid partitioning.

4. Evaluate and Conclude: If neither horizontal nor vertical cuts satisfy the conditions after a complete evaluation, the method returns false, indicating that it is impossible to partition all rectangles into three separate sections according to specifications.

This method efficiently checks possible cuts by leveraging the properties of sorted bounding edges, ensuring that the solution is optimal for the input constraints.

Code

C++

class Solution {
public:
    bool checkValidCuts(int n, vector<vector<int>>& rectangles) {
        int horzMax = INT_MIN, vertMax = INT_MIN;
        vector<int> horz, vert;

        // Extract edges from rectangles and track the maximum x and y
        for (vector<int>& rect : rectangles) {
            horzMax = max(horzMax, rect[2]);
            vertMax = max(vertMax, rect[3]);
            horz.push_back(rect[0]);
            vert.push_back(rect[1]);
            horz.push_back(-rect[2]);
            vert.push_back(-rect[3]);
        }
        
        // Sort edges to check possible cuts
        sort(horz.begin(), horz.end(), [](const int& a, const int& b) {
            if (abs(a) != abs(b)) return abs(a) < abs(b);
            else return a < b;
        });
        sort(vert.begin(), vert.end(), [](const int& a, const int& b) {
            if (abs(a) != abs(b)) return abs(a) < abs(b);
            else return a < b;
        });

        // Check for horizontal cuts
        int horzCuts = 0, activeHorzBlocks = 0;
        for (int i = 0; i < horz.size(); i++) {
            // Adjust active block counter
            if (horz[i] < 0) activeHorzBlocks--;
            else activeHorzBlocks++;
            
            // Check if this point is valid for a cut
            if (activeHorzBlocks == 0 && -horz[i] != horzMax) horzCuts++;
            if (horzCuts >= 2) return true;
        }

        // Check for vertical cuts
        int vertCuts = 0, activeVertBlocks = 0;
        for (int i = 0; i < vert.size(); i++) {
            // Adjust active block counter
            if (vert[i] < 0) activeVertBlocks--;
            else activeVertBlocks++;
            
            // Check if this point is valid for a cut
            if (activeVertBlocks == 0 && -vert[i] != vertMax) vertCuts++;
            if (vertCuts >= 2) return true;
        }

        // Return false if neither horizontal nor vertical cuts are valid
        return false;
    }
};

Python

class Solution:
    def checkValidCuts(self, n, rectangles):
        horzMax = float('-inf')
        vertMax = float('-inf')
        horz = []
        vert = []

        # Extract edges from rectangles and track the maximum x and y
        for rect in rectangles:
            horzMax = max(horzMax, rect[2])
            vertMax = max(vertMax, rect[3])
            horz.append(rect[0])
            vert.append(rect[1])
            horz.append(-rect[2])
            vert.append(-rect[3])
        
        # Sort edges to check possible cuts
        horz.sort(key=lambda a: (abs(a), a))
        vert.sort(key=lambda a: (abs(a), a))

        # Check for horizontal cuts
        horzCuts = 0
        activeHorzBlocks = 0
        for i in range(len(horz)):
            # Adjust active block counter
            if horz[i] < 0:
                activeHorzBlocks -= 1
            else:
                activeHorzBlocks += 1
            
            # Check if this point is valid for a cut
            if activeHorzBlocks == 0 and -horz[i] != horzMax:
                horzCuts += 1
            if horzCuts >= 2:
                return True

        # Check for vertical cuts
        vertCuts = 0
        activeVertBlocks = 0
        for i in range(len(vert)):
            # Adjust active block counter
            if vert[i] < 0:
                activeVertBlocks -= 1
            else:
                activeVertBlocks += 1
            
            # Check if this point is valid for a cut
            if activeVertBlocks == 0 and -vert[i] != vertMax:
                vertCuts += 1
            if vertCuts >= 2:
                return True

        # Return false if neither horizontal nor vertical cuts are valid
        return False

Complexity

• Time complexity: $O(m \log m)$

  1. For loop through rectangles:

     • The loop iterates over each rectangle to gather information about the edges. If there are $m$ rectangles, this step takes $O(m)$ time.

  2. Sorting edges:

     • The lists horz and vert are each populated with twice the number of rectangles (two entries per rectangle). Therefore, both lists have a length of $2m$.
     • Sorting both lists individually takes $O(m \log m)$ time, as sorting requires $O(n \log n)$ time complexity, where $n$ is the number of elements to be sorted.

  3. Check for horizontal and vertical cuts:

     • The loops to check valid horizontal and vertical cuts iterate over the sorted lists, each containing $2m$ elements. Thus, each loop runs in $O(m)$.
     • Therefore, the cutting checks total $O(m)$.

  The dominant factor here is the sorting step, which gives the complete algorithm a time complexity of $O(m \log m)$.

• Space complexity: $O(m)$

  1. Space for edge lists:

     • The lists horz and vert each contain $2m$ integers, where $m$ is the number of rectangles.

  2. Auxiliary storage:

     • Sorting operations and edge lists require additional storage proportional to the size of the list being sorted.

  The overall space complexity is determined by the space required for the edge lists, which is $O(m)$.