Problem Informations

Problem Index: 361
Problem Link: Bomb Enemy
Topics: Array, Dynamic Programming, Matrix

Problem Description

Given an $m \times n$ matrix grid where each cell is either a wall ‘W’, an enemy ‘E’ or empty ‘0’, return the maximum enemies you can kill using one bomb. You can only place the bomb in an empty cell.

The bomb kills all the enemies in the same row and column from the planted point until it hits the wall since it is too strong to be destroyed.

Example 1:

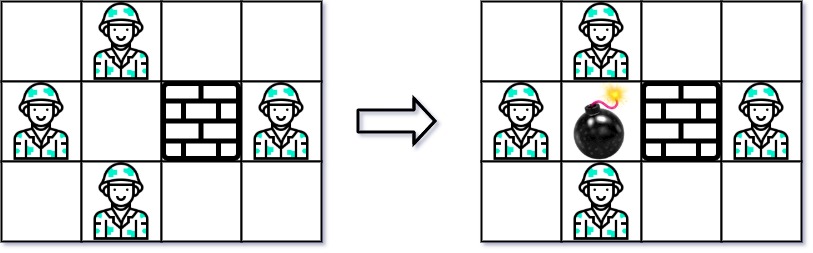
Example 1

Input: grid = [["0","E","0","0"],["E","0","W","E"],["0","E","0","0"]]
Output: 3

Example 2:

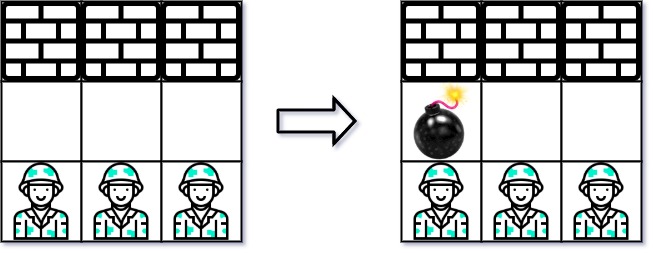
Example 2

Input: grid = [["W","W","W"],["0","0","0"],["E","E","E"]]
Output: 1

Constraints:

$m = \text{grid.length}$
$n = \text{grid}[i].\text{length}$
$1 \leq m, n \leq 500$
$\text{grid}[i][j]$ is either ‘W’, ‘E’, or ‘0’.

Intuition

The problem requires us to determine the maximum number of enemies that can be eliminated by placing a bomb in a particular cell of a grid matrix. Each cell can contain a wall, an enemy, or be empty, and the bomb can only be placed in an empty cell. The bomb will affect all enemies in the same row and column until it encounters a wall, which stops its effect. The goal is to explore the grid and calculate the potential number of enemies that can be killed from each empty cell to optimize the bomb placement.

Approach

The solution is approached by traversing the grid to calculate the number of enemies that can be killed by placing a bomb in the empty cells:

Grid Setup:
- We initialize a matrix killCount of the same size as the input grid to keep track of the number of enemies killed for each empty cell.
Horizontal Sweep:
- For each row, we iterate through the cells. We use a variable enemyCount to accumulate the count of enemies met until a wall ‘W’ or the end of the row is reached.
- Once a wall or the end is encountered, for each empty cell (‘0’) encountered in that segment, we increment its killCount with the accumulated enemyCount.
- Reset enemyCount after a wall or end boundary to start fresh for the next series of cells.
Vertical Sweep:
- Similarly, for each column, we repeat the process by iterating through the column from top to bottom.
- Again, enemyCount is used to count contiguous enemies until a wall or the end of the column.
- For each empty cell encountered in that segment, we add the enemy count to its respective killCount value.
- Reset enemyCount after encountering a wall or column boundary.
Determine Maximum Kills:
- Finally, traverse the killCount matrix to find the maximum value. This value represents the maximum number of enemies that can be killed with one bomb.

This two-pass approach ensures efficient computation of potential kills by leveraging the constraints of the problem, allowing each empty cell to be analyzed for optimal bomb placement without redundant computations. The complexity is $O(m \times n)$, making it feasible for the problem’s constraints.

Code

C++

class Solution {
public:
    int maxKilledEnemies(vector<vector<char>>& grid) {
        int m = grid.size();
        int n = grid[0].size();
        
        // Vector to store the number of enemies that can be killed at each cell
        vector<vector<int>> killCount(m, vector<int>(n, 0));

        // Traverse each row to calculate kills for horizontal attacks
        for (int i = 0; i < m; i++) {
            int past = 0;
            int enemyCount = 0;
            
            while (past < n) {
                for (int j = 0; past + j < n + 1; j++) {
                    if (past + j == n || grid[i][past + j] == 'W') {
                        for (int k = past; k < past + j; k++) {
                            if (grid[i][k] == '0') {
                                killCount[i][k] += enemyCount;
                            }
                        }
                        enemyCount = 0;
                        past += j + 1;
                        break;
                    } else if (grid[i][past + j] == 'E') {
                        enemyCount++;
                    }
                }
            }
        }

        // Traverse each column to calculate kills for vertical attacks
        for (int i = 0; i < n; i++) {
            int past = 0;
            int enemyCount = 0;
            
            while (past < m) {
                for (int j = 0; past + j < m + 1; j++) {
                    if (past + j == m || grid[past + j][i] == 'W') {
                        for (int k = past; k < past + j; k++) {
                            if (grid[k][i] == '0') {
                                killCount[k][i] += enemyCount;
                            }
                        }
                        enemyCount = 0;
                        past += j + 1;
                        break;
                    } else if (grid[past + j][i] == 'E') {
                        enemyCount++;
                    }
                }
            }
        }

        // Find the maximum number of enemies that can be killed with one bomb
        int maxKill = killCount[0][0];
        for (const auto& row : killCount) {
            int rowMax = *max_element(row.begin(), row.end());
            maxKill = max(maxKill, rowMax);
        }

        return maxKill;
    }
};

Python

class Solution:
    def maxKilledEnemies(self, grid):
        m = len(grid)
        n = len(grid[0])
        
        # Vector to store the number of enemies that can be killed at each cell
        killCount = [[0] * n for _ in range(m)]
        
        # Traverse each row to calculate kills for horizontal attacks
        for i in range(m):
            past = 0
            enemyCount = 0
            
            while past < n:
                for j in range(n + 1):
                    if past + j == n or grid[i][past + j] == 'W':
                        for k in range(past, past + j):
                            if grid[i][k] == '0':
                                killCount[i][k] += enemyCount
                        enemyCount = 0
                        past += j + 1
                        break
                    elif grid[i][past + j] == 'E':
                        enemyCount += 1

        # Traverse each column to calculate kills for vertical attacks
        for i in range(n):
            past = 0
            enemyCount = 0
            
            while past < m:
                for j in range(m + 1):
                    if past + j == m or grid[past + j][i] == 'W':
                        for k in range(past, past + j):
                            if grid[k][i] == '0':
                                killCount[k][i] += enemyCount
                        enemyCount = 0
                        past += j + 1
                        break
                    elif grid[past + j][i] == 'E':
                        enemyCount += 1

        # Find the maximum number of enemies that can be killed with one bomb
        maxKill = killCount[0][0]
        for row in killCount:
            rowMax = max(row)
            maxKill = max(maxKill, rowMax)

        return maxKill

Complexity

Time complexity: $O(m \times n)$
The algorithm involves two main traversals of the matrix. For the horizontal attack calculation, each row in the matrix is traversed with a complexity of $O(n)$, where $n$ is the number of columns. Since there are $m$ rows, this part of the algorithm has a complexity of $O(m \times n)$. Similarly, for the vertical attack calculation, each column is traversed with a complexity of $O(m)$, and since there are $n$ columns, this segment of the algorithm also results in a complexity of $O(m \times n)$. Finally, finding the maximum number of enemies that can be killed by one bomb involves a row-wise search with a complexity of $O(m \times n)$. Therefore, the overall time complexity of the algorithm is $O(m \times n)$.
Space complexity: $O(m \times n)$
The space complexity is determined by the killCount vector, which stores the number of enemies that can be killed from each empty cell. This vector has dimensions $m \times n$, corresponding to the size of the input grid. Therefore, the space complexity of the algorithm is $O(m \times n)$.

CS Note
中

Leetcode 361. Bomb Enemy