Problem Informations

• Problem Index: 73
• Problem Link: Set Matrix Zeroes
• Topics: Array, Hash Table, Matrix

Problem Description

Given an $m \times n$ integer matrix $matrix$, if an element is $0$, set its entire row and column to $0$’s.

You must do it in place.

Example 1:

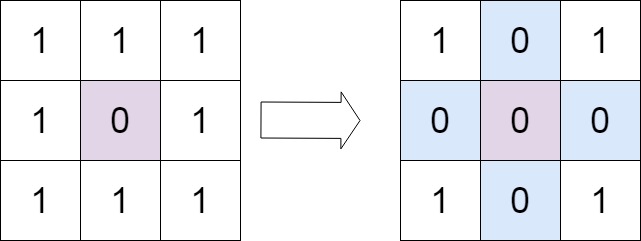
Input: matrix = [[1,1,1],[1,0,1],[1,1,1]]
Output: [[1,0,1],[0,0,0],[1,0,1]]

Example 2:

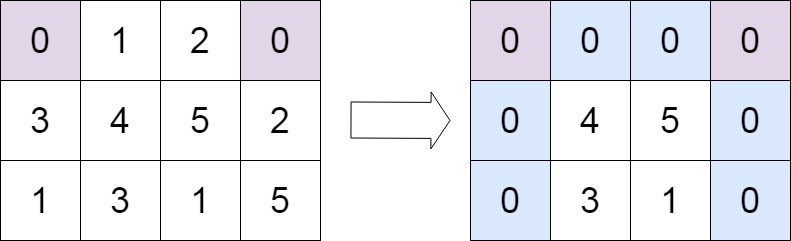
Input: matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
Output: [[0,0,0,0],[0,4,5,0],[0,3,1,0]]

Constraints:

• $m == matrix.length$
• $n == matrix[0].length$
• $1 \leq m, n \leq 200$
• $-2^{31} \leq matrix[i][j] \leq 2^{31} - 1$

Follow up:

• A straightforward solution using $O(mn)$ space is probably a bad idea.
• A simple improvement uses $O(m + n)$ space, but still not the best solution.
• Could you devise a constant space solution?

Intuition

The problem requires us to set an entire row and column to zero if any of its elements is zero. The challenge is to perform this in place without using extra space, meaning we cannot use additional arrays or lists to keep track of which rows and columns need to be zeroed. The main insight is to use the first row and first column of the matrix itself to store this information, while also keeping track of whether the first row originally contains any zeroes. This allows us to ensure all necessary rows and columns are zeroed without additional space.

Approach

Given the constraints and requirements, this problem is best tackled by leveraging the matrix itself to reduce space complexity. Here’s a step-by-step outline of the approach:

1. Initialization: Determine the size of the matrix, m for the number of rows and n for the number of columns. Introduce a Boolean flag firstRowHasZero to check if the first row contains any zeroes initially.

2. First Row Check: Iterate over the first row to check for zeros. If a zero is found, set firstRowHasZero to true. This step helps ensure that after other operations, we can correctly zero out the first row if it originally contained a zero.

3. Mark Rows and Columns: Use a nested loop starting from the second row (index 1) to traverse the matrix. If a zero is encountered at position (i, j), mark the first element of the i-th row and j-th column as zero. This serves as an indicator that the entire i-th row and j-th column should eventually be zeroed.

4. Zero Rows: After setting markers, iterate through rows starting from the second row again. If the first element of a row is zero, set all elements in that row to zero.

5. Zero Columns: Similarly, traverse columns starting from the first column. If the first element of a column is zero, set all elements in that column to zero.

6. Update First Row if Needed: In the end, if firstRowHasZero is true, zero out the entire first row to account for any zeroes that were initially present.

This method efficiently handles the zero-marking process using constant space, since modifications are directly applied to the input matrix itself. The approach ensures that the matrix is altered in place, satisfying the constraints of the problem.

Code

C++

class Solution {
public:
    void setZeroes(vector<vector<int>>& matrix) {
        int m = matrix.size(); // Number of rows in the matrix
        int n = matrix[0].size(); // Number of columns in the matrix
        bool firstRowHasZero = false; // Flag to check if the first row has any zero

        // Check the first row for any zero and set the flag accordingly
        for (int col = 0; col < n; ++col) {
            if (matrix[0][col] == 0) {
                firstRowHasZero = true;
                break;
            }
        }

        // Use the first row and first column as markers for rows and columns to be zeroed
        for (int row = 1; row < m; ++row) {
            for (int col = 0; col < n; ++col) {
                if (matrix[row][col] == 0) {
                    matrix[0][col] = 0; // Mark the column
                    matrix[row][0] = 0; // Mark the row
                }
            }
        }

        // Zero out the cells based on the markers in the first column
        for (int row = 1; row < m; ++row) {
            if (matrix[row][0] == 0) {
                for (int col = 1; col < n; ++col) {
                    matrix[row][col] = 0;
                }
            }
        }

        // Zero out the cells based on the markers in the first row
        for (int col = 0; col < n; ++col) {
            if (matrix[0][col] == 0) {
                for (int row = 1; row < m; ++row) {
                    matrix[row][col] = 0;
                }
            }
        }

        // If the first row originally had zero, zero out the entire first row
        if (firstRowHasZero) {
            for (int col = 0; col < n; ++col) {
                matrix[0][col] = 0;
            }
        }
    }
};

Python

class Solution:
    def setZeroes(self, matrix):
        m = len(matrix)  # Number of rows in the matrix
        n = len(matrix[0])  # Number of columns in the matrix
        firstRowHasZero = False  # Flag to check if the first row has any zero

        # Check the first row for any zero and set the flag accordingly
        for col in range(n):
            if matrix[0][col] == 0:
                firstRowHasZero = True
                break

        # Use the first row and first column as markers for rows and columns to be zeroed
        for row in range(1, m):
            for col in range(n):
                if matrix[row][col] == 0:
                    matrix[0][col] = 0  # Mark the column
                    matrix[row][0] = 0  # Mark the row

        # Zero out the cells based on the markers in the first column
        for row in range(1, m):
            if matrix[row][0] == 0:
                for col in range(1, n):
                    matrix[row][col] = 0

        # Zero out the cells based on the markers in the first row
        for col in range(n):
            if matrix[0][col] == 0:
                for row in range(1, m):
                    matrix[row][col] = 0

        # If the first row originally had zero, zero out the entire first row
        if firstRowHasZero:
            for col in range(n):
                matrix[0][col] = 0

Complexity

• Time complexity: The algorithm traverses the matrix several times, each with a complexity of $O(m \times n)$ due to full or partial scans of the matrix. Since it does not exceed these layered operations, the time complexity is $O(m \times n)$.

• Space complexity: The solution uses a constant amount of extra space, denoted by $O(1)$. This is due to the use of only a few additional variables (firstRowHasZero) and in-place modification of the matrix without additional data structures.