Problem Informations

• Problem Index: 790
• Problem Link: Domino and Tromino Tiling
• Topics: Dynamic Programming

Problem Description

You have two types of tiles: a 2 x 1 domino shape and a tromino shape. You may rotate these shapes.

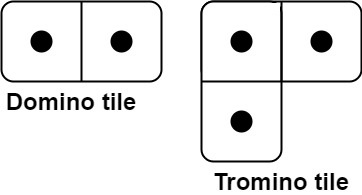
Given an integer $n$, return the number of ways to tile an 2 x n board. Since the answer may be very large, return it modulo $10^9 + 7$.

In a tiling, every square must be covered by a tile. Two tilings are different if and only if there are two 4-directionally adjacent cells on the board such that exactly one of the tilings has both squares occupied by a tile.

Example 1:

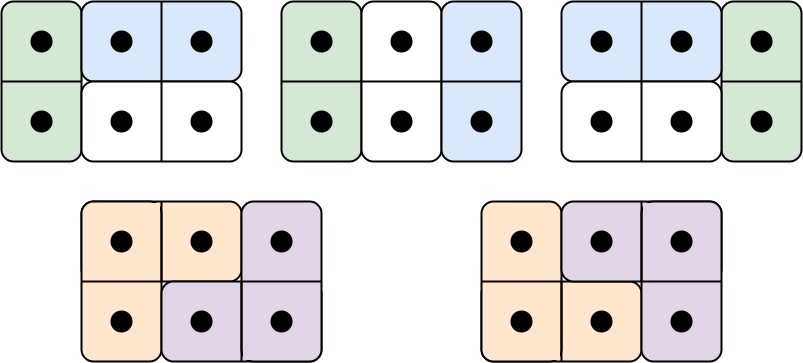
Input: n = 3
Output: 5
Explanation: The five different ways are show above.

Example 2:

Input: n = 1
Output: 1

Constraints:

• $1 \leq n \leq 1000$

Intuition

The problem of tiling a 2 x n board with domino and tromino shapes can be framed using dynamic programming. The main realization is that the number of ways to tile the board depends on previously computed solutions for smaller board sizes. Understanding how differently the domino and tromino shapes can fill parts of the board allows us to recursively build the solution from smaller cases. The recursion captures that a 2 x n board can be thought of being formed by extending a smaller board (2 x (n-1), 2 x (n-2), or 2 x (n-3)). This approach results from visualizing the tiling constructions that lead to different configurations based on the last few tiles placed.

Approach

To solve the tiling problem, we employ dynamic programming to compute the number of configurations for each board size from 1 to n, and store the results to avoid redundant calculations. Here is a detailed explanation of the approach:

1. Base Cases:

   • When n = 1, there is only one way to tile a 2 x 1 board, which is using a single vertical domino. Thus, dp[1] = 1.
   • For n = 2, the board can be tiled in two ways: either by placing two vertical dominoes side by side or two horizontal dominoes stacked. Hence, dp[2] = 2.
   • For n = 3, five different tiling configurations arise which include both dominoes and trominos. Thus, dp[3] = 5.

2. State Transition:

   • For any board of size 2 x i where i > 3, the board can be constructed from:
     • A 2 x (i-1) board extended by placing an additional vertical domino at the end.
     • A 2 x (i-2) board extended by adding two horizontal dominoes to complete the 2 x 2 section.
     • A 2 x (i-3) board extended by adding a tromino in one of its forms.
   • The recursive formula is derived as: $$ dp[i] = (2 \times dp[i - 1] + dp[i - 3]) \mod (10^9 + 7) $$

3. Dynamic Programming Array Construction:

   • We initialize a dynamic programming (DP) array dp where dp[i] will represent the number of ways to tile a 2 x i board.
   • We prepopulate the dp array with the base cases.
   • We iterate from i = 4 to n, applying the transition formula to fill up the DP array with results for each subsequent board size.

4. Result Computation:

   • After populating the DP array, the solution for a 2 x n board is stored in dp[n].
   • Return dp[n] as the final answer modulo (10^9 + 7) to handle large numbers while preventing overflow.

This approach efficiently computes the number of possible tiling configurations by leveraging previously computed results, reducing the complexity through dynamic programming.

Code

C++

class Solution {
    // Define the modulo as a constant to handle large numbers
    int MOD = 1000000007;
    
public:
    int numTilings(int n) {
        // Base cases for small n
        if (n <= 1) return 1;
        if (n == 2) return 2;
        if (n == 3) return 5;
        
        // Create a dynamic programming array to store results
        vector<int> dp(n + 1, 0);
        dp[0] = 1; // There is one way to tile a 2x0 board (do nothing)
        dp[1] = 1; // One way to tile a 2x1 board (using one vertical domino)
        dp[2] = 2; // Two ways to tile a 2x2 board (two vertical dominos or two horizontal dominos)
        dp[3] = 5; // Five ways to tile a 2x3 board as explained earlier
        
        // Use dynamic programming to fill the dp array for all boards up to 2xn
        for (int i = 4; i <= n; ++i) {
            // Calculate number of ways for a 2xi board using previously computed values
            dp[i] = ((long long)dp[i - 1] * 2 + (long long)dp[i - 3]) % MOD; 
        }
        
        // Return the result for the specific input n
        return dp[n];
    }
};

Python

class Solution:
    # Define the modulo as a constant to handle large numbers
    MOD = 1000000007
    
    def numTilings(self, n: int) -> int:
        # Base cases for small n
        if n <= 1:
            return 1
        if n == 2:
            return 2
        if n == 3:
            return 5
        
        # Create a dynamic programming array to store results
        dp = [0] * (n + 1)
        dp[0] = 1  # There is one way to tile a 2x0 board (do nothing)
        dp[1] = 1  # One way to tile a 2x1 board (using one vertical domino)
        dp[2] = 2  # Two ways to tile a 2x2 board (two vertical dominos or two horizontal dominos)
        dp[3] = 5  # Five ways to tile a 2x3 board as explained earlier
        
        # Use dynamic programming to fill the dp array for all boards up to 2xn
        for i in range(4, n + 1):
            # Calculate number of ways for a 2xi board using previously computed values
            dp[i] = (dp[i - 1] * 2 + dp[i - 3]) % self.MOD
        
        # Return the result for the specific input n
        return dp[n]

Complexity

• Time complexity: The time complexity of the algorithm is $O(n)$. This is because the algorithm uses a single loop that iterates over a range from 4 to $n$, and within each iteration, a constant amount of work is performed.

• Space complexity: The space complexity of the algorithm is $O(n)$. This is due to the dynamic programming array dp which stores solutions for all board sizes from 0 to $n$. The length of this array is $n+1$, leading to a space complexity of $O(n)$.