Problem Informations

• Problem Index: 865
• Problem Link: Smallest Subtree with all the Deepest Nodes
• Topics: Hash Table, Tree, Depth-First Search, Breadth-First Search, Binary Tree

Problem Description

Given the root of a binary tree, the depth of each node is the shortest distance to the root.

Return the smallest subtree such that it contains all the deepest nodes in the original tree.

A node is called the deepest if it has the largest depth possible among any node in the entire tree.

The subtree of a node is a tree consisting of that node, plus the set of all descendants of that node.

Example 1:

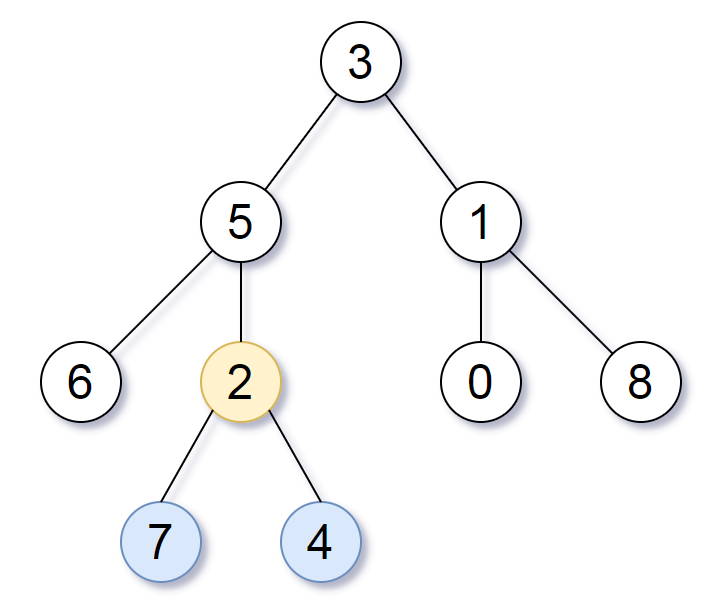
Input: root = [3,5,1,6,2,0,8,null,null,7,4]
Output: [2,7,4]
Explanation: We return the node with value 2, colored in yellow in the diagram.
The nodes coloured in blue are the deepest nodes of the tree.
Notice that nodes 5, 3 and 2 contain the deepest nodes in the tree but node 2 is the smallest subtree among them, so we return it.

Example 2:

Input: root = [1]
Output: [1]
Explanation: The root is the deepest node in the tree.

Example 3:

Input: root = [0,1,3,null,2]
Output: [2]
Explanation: The deepest node in the tree is 2, the valid subtrees are the subtrees of nodes 2, 1 and 0 but the subtree of node 2 is the smallest.

Constraints:

• The number of nodes in the tree will be in the range $[1, 500]$.
• $0 \leq \text{Node.val} \leq 500$
• The values of the nodes in the tree are unique.

Note: This question is the same as 1123: https://leetcode.com/problems/lowest-common-ancestor-of-deepest-leaves/

Intuition

The problem requires finding the smallest subtree containing all of the deepest nodes in a given binary tree. A straightforward approach involves using depth-first search (DFS) to traverse the tree and gather information about the depth of each node. By determining the deepest nodes and evaluating the tree structure, we can effectively pinpoint the desired subtree. The essential insight is to recognize the subtree that envelopes all deepest nodes, which is equivalent to finding the lowest common ancestor (LCA) of these nodes.

Approach

The algorithm employs a depth-first search (DFS) to analyze the binary tree. The primary challenge is to find the smallest subtree that includes all nodes with the maximum depth. The recursive DFS function executes the following steps:

1. Base Case: If the node is nullptr, return a pair consisting of nullptr and depth 0. This represents noting an absence of a node at this position.

2. Recursive Search: For each node, recursively call the DFS function on the left and right children to calculate and retrieve information about their deepest nodes and their respective depths, encapsulated in pairs.

3. Depth Comparison:

   • If the left subtree contains nodes with a greater depth than the right subtree, return the information from the left, incremented by one to account for the current node’s depth.
   • Conversely, if the right side is deeper, return data from the right side, similarly incremented.
   • In scenarios where both left and right subtrees have equivalent depths, it signifies that the current node is the common ancestor for the deepest nodes identified from both subtrees. Return the current node along with its depth.

4. Solution Extraction: Commence the DFS traversal starting from the root node. The node returned by this traversal embodies the root of the smallest subtree containing all the deepest nodes.

This method efficiently pinpoints the required subtree by evaluating the depths of subtrees and leveraging the properties of the binary tree to conclude the presence and position of the deepest nodes.

Code

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */

class Solution {
public:
    // Depth-first search to find the deepest subtree and its depth.
    pair<TreeNode*, int> dfs(TreeNode* node) {
        // Base case: if the current node is null, return a pair of nullptr and depth 0.
        if (node == nullptr) return {nullptr, 0};
        
        // Recursively calculate the deepest node info for the left and right subtrees.
        pair<TreeNode*, int> left_info = dfs(node->left);
        pair<TreeNode*, int> right_info = dfs(node->right);
        
        // Compare depths of left and right subtrees.
        if (left_info.second > right_info.second)
            return {left_info.first, left_info.second + 1};  // Left subtree is deeper.
        else if (left_info.second < right_info.second)
            return {right_info.first, right_info.second + 1}; // Right subtree is deeper.
        else
            return {node, left_info.second + 1}; // Both subtrees have the same depth.
    }

    // Function to find the smallest subtree containing all the deepest nodes.
    TreeNode* subtreeWithAllDeepest(TreeNode* root) {
        return dfs(root).first;
    }
};

Python

# Definition for a binary tree node.
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class Solution:
    # Depth-first search to find the deepest subtree and its depth.
    def dfs(self, node):
        # Base case: if the current node is null, return a tuple of None and depth 0.
        if node is None:
            return (None, 0)
        
        # Recursively calculate the deepest node info for the left and right subtrees.
        left_info = self.dfs(node.left)
        right_info = self.dfs(node.right)
        
        # Compare depths of left and right subtrees.
        if left_info[1] > right_info[1]:
            return (left_info[0], left_info[1] + 1)  # Left subtree is deeper.
        elif left_info[1] < right_info[1]:
            return (right_info[0], right_info[1] + 1) # Right subtree is deeper.
        else:
            return (node, left_info[1] + 1) # Both subtrees have the same depth.

    # Function to find the smallest subtree containing all the deepest nodes.
    def subtreeWithAllDeepest(self, root):
        return self.dfs(root)[0]

Complexity

• Time complexity: $O(n)$

  The given solution involves a depth-first search (DFS) traversal of the binary tree. Each node in the tree is visited once to calculate the depth and determine the deepest subtree. Hence, the time complexity is $O(n)$, where $n$ is the number of nodes in the tree.

• Space complexity: $O(h)$

  The space complexity is determined by the recursion stack used in the DFS traversal. In the worst case, the height of the tree could be $n$ (in case of a skewed tree), leading to a space complexity of $O(n)$. However, for a balanced tree, the height is $O(\log n)$. Therefore, the space complexity is $O(h)$, where $h$ is the height of the tree.