題目資訊

題目編號: 1976
題目連結: Number of Ways to Arrive at Destination
主題: Dynamic Programming, Graph, Topological Sort, Shortest Path

題目敘述

你所在的城市由 $n$ 個交通路口組成，編號從 $0$ 到 $n - 1$，並且在某些路口之間有雙向道路。這些輸入數據被設計成可以從任何路口到達其他任何路口，且任意兩個路口之間最多只有一條道路。

給定一個整數 $n$ 和一個 2D 整數數組 $roads$，其中 $roads[i] = [u_i, v_i, time_i]$ 表示在路口 $u_i$ 和 $v_i$ 之間有一條道路，耗費 $time_i$ 分鐘。你需要知道從路口 $0$ 到路口 $n - 1$ 能以最短時間到達的方式有多少種。

返回能以最短時間到達目的地的方式數量。由於答案可能會很大，請返回對 $10^9 + 7$ 取模的結果。

範例 1:

範例 1

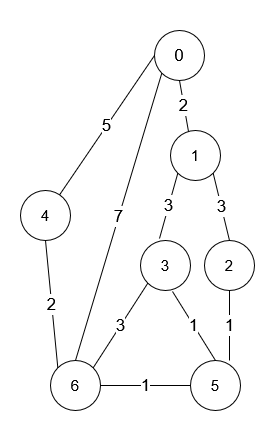
輸入: n = 7, roads = [[0,6,7],[0,1,2],[1,2,3],[1,3,3],[6,3,3],[3,5,1],[6,5,1],[2,5,1],[0,4,5],[4,6,2]]
輸出: 4
解釋: 從路口 0 到路口 6 最短所需的時間是 7 分鐘。
在 7 分鐘內到達的四種方式是:
- 0 ➝ 6
- 0 ➝ 4 ➝ 6
- 0 ➝ 1 ➝ 2 ➝ 5 ➝ 6
- 0 ➝ 1 ➝ 3 ➝ 5 ➝ 6

範例 2:

輸入: n = 2, roads = [[1,0,10]]
輸出: 1
解釋: 從路口 0 到路口 1 只有一種方式，耗時 10 分鐘。

約束條件:

$1 \leq n \leq 200$
$n - 1 \leq roads.length \leq \frac{n \cdot (n - 1)}{2}$
$roads[i].length == 3$
$0 \leq u_i, v_i \leq n - 1$
$1 \leq time_i \leq 10^9$
$u_i \neq v_i$
任意兩個路口之間最多只有一條道路連接。
你可以從任何路口到達其他任何路口。

直覺

此問題本質上是一個圖遍歷問題，我們需要找出從起始節點（交叉點 0）到目標節點（交叉點 ( n-1 )）的最短路徑，同時也要計算有多少條不同的路徑可以達到該最短時間。解決此問題的主要直覺是利用圖遍歷技術來首先找出從起始節點到所有其他節點的最短路徑距離，然後計算構建這些最短路徑的不同方式數量。

解法

解決此問題的方法分為兩個主要部分：計算最短路徑及計算不同最短路徑的數量。

圖的表示：城市和道路透過鄰接表表示，其中每個節點都有一個其相鄰節點的列表以及沿著這些道路旅行所需的時間。
初始化：
- 我們維護一個距離陣列 (dp)，記錄從起點交叉節點（節點 0）到每個節點的最短距離，初始值設為無窮大（LLONG_MAX），表示節點最初是無法到達的。
- 另一個陣列 (ways) 保持用最短路徑到達每個節點的方式數量，初始為 -1，表示方式數量尚未計算。
找出最短路徑：
- 我們使用遞迴函數 findShortestPaths，通過更新距離陣列 dp 來確定從起始節點（0）到每個其他節點的最短路徑。
- 我們通過圖進行深度優先遍歷。如果發現到某節點的更短路徑，則更新其距離，並遞迴繼續對其相鄰節點進行遍歷。
計算方式數量：
- 透過動態規劃方法，使用 computeWays 函數計算到達目標節點（n-1）的最短路徑數量。
- 基本情況：直接在起始節點（0），有一種方式使用最短路徑，因此 ways[0] 為 1。
- 對於每個節點，函數通過匯聚來自相連節點的路徑數量來計算方式數量，前提是這些節點位於構成當前節點最短路徑的最短路徑上（dp[neighbor.first] + neighbor.second == dp[index]）。
- 結果以 (10^9 + 7) 取模，處理問題要求的大數。
最終計算：
- 我們從節點 0 開始調用 findShortestPaths 來啟動過程。
- 在確定所有最短路徑距離後，調用 computeWays 計算目標節點 n-1，得出從節點 0 到節點 n-1 的不同最短路徑數量。

通過結合這些步驟，我們計算出到達目的地的最短時間以及達到該最短時間的不同方式數量。此方法有效地利用深度優先搜索來進行最短路徑的確定以及動態規劃來計算路徑數量。

程式碼

C++

class Solution {
public:
    // 定義常數
    static const long long MOD = 1e9 + 7;
    
    // 資料成員用來儲存方法數量、最短路徑和鄰接表
    long long ans;
    vector<long long> dp;
    vector<long long> ways;
    vector<vector<pair<long long, long long>>> adjacencyList;

    // 從起始索引尋找到所有其他節點的最短路徑的函式
    void findShortestPaths(long long index, long long length) {
        // 如果當前路徑更短，更新最短路徑
        if (dp[index] > length) {
            dp[index] = length;
            // 遞迴地尋找連接節點的最短路徑
            for (const pair<long long, long long>& neighbor : adjacencyList[index]) {
                findShortestPaths(neighbor.first, length + neighbor.second);
            }
        }
    }

    // 計算以最短時間到達目的地的方法數量的函式
    long long computeWays(long long index) {
        // 基本情況：起始點
        if (index == 0) return 1;
        // 如果有預先計算的方法，則返回
        if (ways[index] != -1) return ways[index];

        ways[index] = 0;
        // 分析每個連接的節點
        for (const pair<long long, long long>& neighbor : adjacencyList[index]) {
            // 如果路徑是一部分的最短路線，從該節點添加方法
            if (dp[neighbor.first] + neighbor.second == dp[index]) {
                ways[index] = (ways[index] + computeWays(neighbor.first)) % MOD;
            }
        }
        return ways[index];
    }

    // 主函式來計算路徑的數量
    int countPaths(int n, vector<vector<int>>& roads) {
        // 初始化變數
        ans = 0;
        dp.clear();
        dp.resize(n, LLONG_MAX);
        ways.clear();
        ways.resize(n, -1);

        // 初始化鄰接表
        adjacencyList.clear();
        adjacencyList.resize(n);

        // 使用道路資料填充鄰接表
        for (const vector<int>& road : roads) {
            adjacencyList[road[0]].emplace_back(road[1], road[2]);
            adjacencyList[road[1]].emplace_back(road[0], road[2]);
        }

        // 從索引0開始尋找最短路徑
        findShortestPaths(0, 0);
        // 計算在最短路徑中到達目的地的方法
        return computeWays(n - 1);
    }
};

Python

class Solution:
    # 定義常數
    MOD = int(1e9 + 7)
    
    # 成員變數來儲存路徑數量、最短路徑和鄰接表
    ans = 0
    dp = []
    ways = []
    adjacencyList = []

    # 函數用來找出從起始索引到所有其他節點的最短路徑
    def findShortestPaths(self, index, length):
        # 如果當前路徑較短，更新最短路徑
        if self.dp[index] > length:
            self.dp[index] = length
            # 遞迴地找出連接節點的最短路徑
            for neighbor in self.adjacencyList[index]:
                self.findShortestPaths(neighbor[0], length + neighbor[1])

    # 函數用來計算以最短時間到達目的地的方法數
    def computeWays(self, index):
        # 基本情況：起始點
        if index == 0:
            return 1
        # 如果有預計算過的方法數，則返回
        if self.ways[index] != -1:
            return self.ways[index]

        self.ways[index] = 0
        # 分析每個連接的節點
        for neighbor in self.adjacencyList[index]:
            # 如果路徑是最短路徑的一部分，則加入從該節點的方法數
            if self.dp[neighbor[0]] + neighbor[1] == self.dp[index]:
                self.ways[index] = (self.ways[index] + self.computeWays(neighbor[0])) % self.MOD
        return self.ways[index]

    # 主要函數，用於計算路徑數量
    def countPaths(self, n, roads):
        # 初始化變數
        self.ans = 0
        self.dp = [float('inf')] * n
        self.ways = [-1] * n

        # 初始化鄰接表
        self.adjacencyList = [[] for _ in range(n)]

        # 使用道路數據填充鄰接表
        for road in roads:
            self.adjacencyList[road[0]].append((road[1], road[2]))
            self.adjacencyList[road[1]].append((road[0], road[2]))

        # 找出從索引0的最短路徑
        self.findShortestPaths(0, 0)
        # 計算在最短路徑中到達目的地的方法數
        return self.computeWays(n - 1)

複雜度分析

時間複雜度： 這個演算法的整體時間複雜度是 $O(n^2)$，其中 $n$ 是交叉路口的數量。findShortestPaths 函數涉及圖形的遞迴遍歷，實際上是在連通圖上實現類似深度優先搜索的方法，在最壞情況下需要 $O(n^2)$ 的時間，這是由於對每個可能的邊緣進行遞迴探索和更新操作。雖然圖形遍歷和邊緣探索最初可能看起來是 $O(E)$，但該函數基本上是反覆重新計算路徑和比較，考慮到在受約束限制的完整場景中 $E \approx n^2$，這導致 $O(n^2)$。computeWays 函數也以類似的遍歷方式運行，涉及潛在路徑檢查，但已經建立了最短路徑模式來優化 $O(n^2)$ 操作。因此，這兩種操作都有助於產生與 $O(n^2)$ 成比例的結果複雜度，全面涵蓋有限空間內的遍歷和更新操作。
空間複雜度： 這個演算法的空間複雜度是 $O(n + E)$，其中 $n$ 是交叉路口的數量，$E$ 是道路（邊緣）的數量。主要貢獻於空間使用的數據結構是向量 dp 和 ways，每個分別佔用 $O(n)$ 空間，用於存儲最短路徑長度和以最短時間到達每個交叉路口的方式數量。此外，鄰接列表 adjacencyList 使用 $O(E)$ 空間來存儲所有道路，表示為每個交叉路口節點的列表中的對。由於在提到的約束下，最大 $E$ 可以接近 $O(n^2)$，因此總體空間需求受到結合 $O(n + E)$ 的限制。

CS Note
En

Leetcode 1976. Number of Ways to Arrive at Destination

題目資訊

題目敘述

直覺

解法

程式碼

C++

Python

複雜度分析