題目資訊

• 題目編號: 2579
• 題目連結: Count Total Number of Colored Cells
• 主題: Math

題目敘述

存在一個無限大的二維網格，由未著色的單位小格組成。給定一個正整數 $n$，表示你必須在 $n$ 分鐘內執行以下操作：

• 第 1 分鐘，將任意一個單位小格塗成藍色。
• 從第二分鐘起，每分鐘將每個與藍色小格相連接的未著色小格塗成藍色。

下面是經過 1、2 和 3 分鐘後網格狀態的圖示。

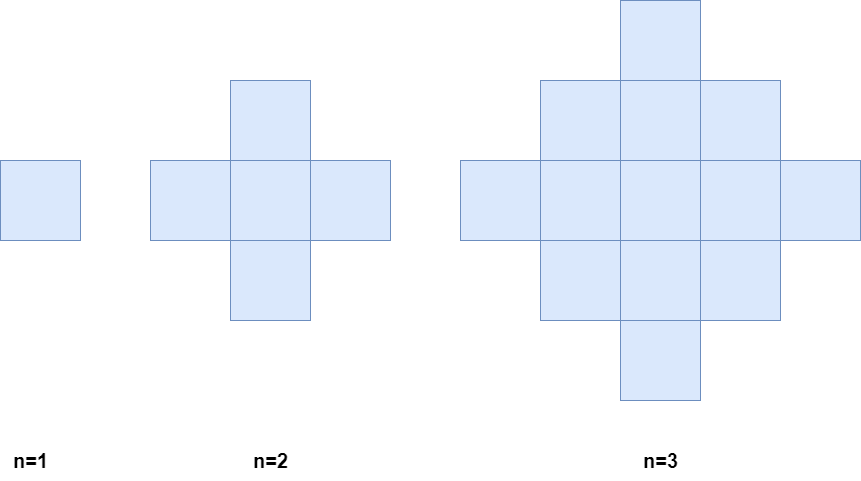
返回 在 $n$ 分鐘結束時的著色小格數量。

例子 1:

輸入: n = 1
輸出: 1
解釋: 經過 1 分鐘後，只有 1 個藍色小格，因此返回 1。

例子 2:

輸入: n = 2
輸出: 5
解釋: 經過 2 分鐘後，邊界上有 4 個著色小格，中心有 1 個，因此返回 5。

約束條件:

• $1 \leq n \leq 10^5$

直覺

此問題主要涉及動態著色網格隨時間步驟的變化。最初，在第一分鐘時，單個單元格被著色，並且在隨後的每分鐘，每個與已著色單元格相鄰的未著色單元格也將被著色。挑戰在於確定在指定的分鐘數 $n$ 之後，被著色單元格的總數。

在分析增長模式後，可以明確看到新著色的單元格以同心層的形式圍繞最初的著色單元格。因此，新著色單元格的數量形成了一個對稱的模式，可以通過數學計算而非迭代模擬網格得到。

解法

為了有效地解決此問題，我們集中於觀察網格模式並推出一個公式：

1. 初始觀察:

   • 在第一分鐘，只有初始單元格被著色，因此總共1個單元格被著色。

2. 增長模式:

   • 從第二分鐘開始，著色區域向外擴展，形成一個以中心單元格為中心的菱形模式。這意味著，對於每一增加的分鐘，新的單元格在四個方向（上、下、左、右）被著色，並形成擴展菱形形狀的邊界。
   • 在第二分鐘，原始單元格有4個相鄰單元格被著色，總共使5個單元格被著色。
   • 擴展此模式，在每分鐘 $k$ 時，額外的邊界單元格數量增加 $4 \times (k - 1)$ 個單元格。

3. 一般公式:

   • 到第 $n$ 分鐘時，新增著色單元格的數量是一個算術級數的和：$4 \times \sum_{k=1}^{n-1} k = 2 \times n \times (n - 1)$。
   • 加上初始單元格，第 $n$ 分鐘時著色單元格的總數為： $$ \text{Total colored cells} = 2 \times n \times (n - 1) + 1 $$

4. 結論:

   • 此方法提供了一個直接計算經過 $n$ 分鐘後著色單元格數的方法，無需模擬網格上的增長過程，特別是在約束條件為 $1 \leq n \leq 10^5$ 的情況下極為有效。

程式碼

C++

class Solution {
public:
    // 這個函式計算在 'n' 分鐘後有多少個被塗色的單元格
    long long coloredCells(int n) {
        // 公式 2 * n * (n - 1) + 1 計算被塗色的單元格總數。
        // 這裡，2 * n * (n - 1) 計算隨時間被塗色的邊界單元格數，
        // 然後我們加上開始時塗色的中心單元格的 1。
        return static_cast<long long>(2) * n * (n - 1) + 1;
    }
};

Python

class Solution:
    # 此函數計算 'n' 分鐘後的著色單元格數量
    def coloredCells(self, n: int) -> int:
        # 公式 2 * n * (n - 1) + 1 計算總著色單元格數量。
        # 其中，2 * n * (n - 1) 計算隨時間著色的邊界單元格數量，
        # 並加上開始時著色的初始中心單元格。
        return 2 * n * (n - 1) + 1

複雜度分析

• 時間複雜度: $O(1)$

  此函數使用直接的數學公式計算著色單元的數量。它僅涉及一些基本的算術運算（乘法和加法），每個運算都需要常數時間。因此，整體的時間複雜度是 $O(1)$。

• 空間複雜度: $O(1)$

  此函數使用常量的空間來儲存變量並執行算術運算。它不需要隨著輸入大小 $n$ 增長的額外空間。因此，空間複雜度是 $O(1)$。