題目資訊

• 題目編號: 3068
• 題目連結: Find the Maximum Sum of Node Values
• 主題: Array, Dynamic Programming, Greedy, Bit Manipulation, Tree, Sorting

題目敘述

存在一棵有 $n$ 個節點的無向樹，節點編號從 $0$ 到 $n - 1$。給定一個長度為 $n - 1$ 的0-索引二維整數數組 edges，其中 edges[i] = [u_i, v_i] 表示在樹中節點 $u_i$ 和 $v_i$ 之間存在一條邊。此外，還給定一個正整數 $k$，以及長度為 $n$ 的0-索引的非負整數數組 nums，其中 nums[i] 表示編號為 $i$ 的節點的值。

Alice 希望樹節點的值的總和達到最大，為此 Alice 可以在樹上進行以下操作任意次（包括零次）：

• 選擇任意連接節點 $u$ 和 $v$ 的邊 [u, v]，並如下更新它們的值：
  • nums[u] = nums[u] XOR k
  • nums[v] = nums[v] XOR k

返回 Alice 通過執行該操作任意次能夠達到的值的總和的最大可能結果。

範例 1:

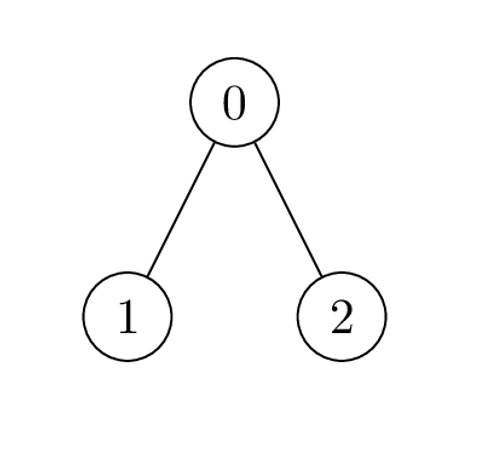
輸入: nums = [1,2,1], k = 3, edges = [[0,1],[0,2]]
輸出: 6
解釋: Alice 可以通過一次操作達到最大總和 6：
- 選擇邊 [0,2]。 nums[0] 和 nums[2] 變為：1 XOR 3 = 2，數組 nums 變為：[1,2,1] -> [2,2,2]。
值的總和是 2 + 2 + 2 = 6。
可以證明 6 是能夠達到的最大值的總和。

範例 2:

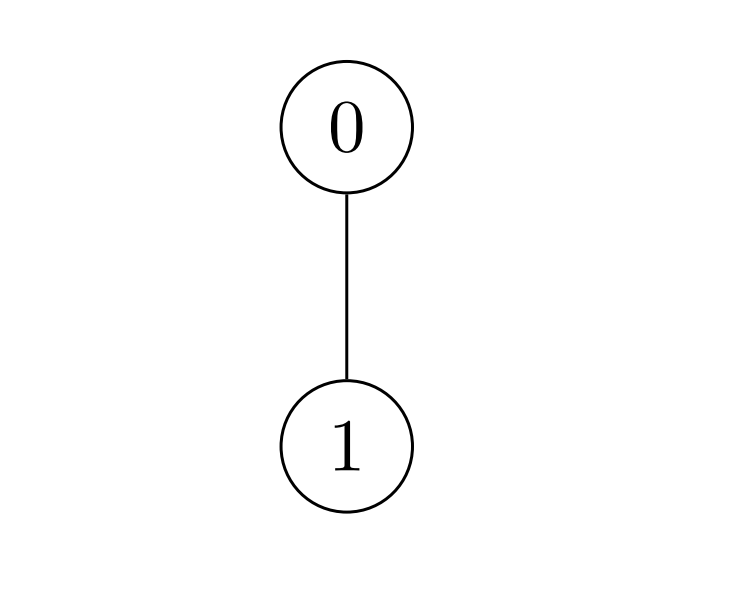
輸入: nums = [2,3], k = 7, edges = [[0,1]]
輸出: 9
解釋: Alice 可以通過一次操作達到最大總和 9：
- 選擇邊 [0,1]。 nums[0] 變為：2 XOR 7 = 5，nums[1] 變為：3 XOR 7 = 4，數組 nums 變為：[2,3] -> [5,4]。
值的總和是 5 + 4 = 9。
可以證明 9 是能夠達到的最大值的總和。

範例 3:

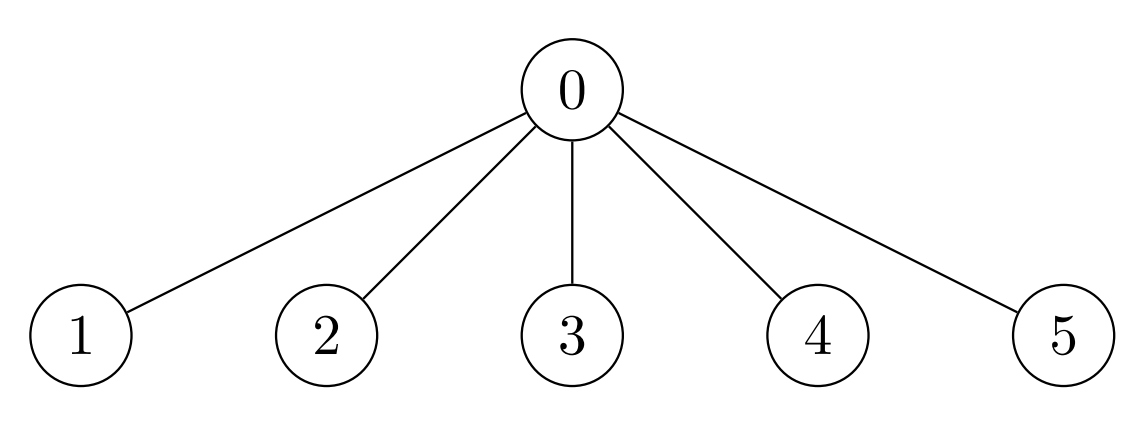
輸入: nums = [7,7,7,7,7,7], k = 3, edges = [[0,1],[0,2],[0,3],[0,4],[0,5]]
輸出: 42
解釋: 最大可達到的總和是 42，這可以通過 Alice 不進行任何操作達成。

約束條件:

• $2 \leq n == \text{nums.length} \leq 2 \times 10^4$
• $1 \leq k \leq 10^9$
• $0 \leq \text{nums}[i] \leq 10^9$
• $\text{edges.length} == n - 1$
• $\text{edges}[i].length == 2$
• $0 \leq \text{edges}[i][0], \text{edges}[i][1] \leq n - 1$
• 輸入生成的 edges 確保表示一棵有效的樹。

直覺

這個問題涉及在無向樹中找到節點值的最大可能總和，這是透過若干次的異或（XOR）操作後的結果。每一次操作在一條邊上會影響相連節點的值。問題的內在挑戰在於選擇哪些操作（如果有的話）能夠使節點值的總和最大化。XOR 操作會切換位元，可能會增加或減少節點值。因此，至關重要的是要策略性地安排哪些操作能產生有益的結果。

解法

為了最大化樹中節點值的總和，我們採用以下策略解決問題：

1. 初始計算：我們遍歷樹中的每個節點，以確定原始節點值（originalValue）和異或操作後乘以 k 的值（flippedValue）。

2. 最大化節點貢獻：對於每個節點，我們決定是使用其原始值還是異或後的值，這取決於哪個較大。這個選擇將直接貢獻於 totalMaxSum，目的是捕獲可能的最大總和。

3. 追蹤最小翻轉差異：在遍歷的同時，我們還監控 minFlipDifference，這表示節點的原始值和翻轉值之間的最小的絕對差異。這一差異是關鍵，因為它有助於在需要調整翻轉時確定最佳的條件。

4. 有益翻轉計數：對於每個節點，我們利用一個 XOR 操作來追蹤 flipCount，這是有益翻轉的衡量標準。如果 flippedValue 大於 originalValue，則一個翻轉被認為是有益的。我們用 flippedValue > originalValue 的布林結果與 flipCount 進行異或，確保 flipCount 在有益翻轉時表示奇數次。

5. 最終調整：在遍歷完成後，我們通過考慮 minFlipDifference 和 flipCount 來調整 totalMaxSum。如果有益操作的次數是奇數，我們減去可能的最小差異，以確保避免不必要的次優翻轉。

這個解法利用了 XOR 操作的特點有效地在樹的邊上切換節點值。透過保持對差異和計數的策略性監控，該演算法保證了最佳結果，而不需要探索所有可能的組合。

程式碼

C++

class Solution {
public:
    // 函數返回兩個 long long 數字中的較小值。
    long long minValue(long long a, long long b) { 
        return (a < b) ? a : b; 
    }
    
    // 函數計算通過翻轉邊緣獲得的最大可能值和。
    long long maximumValueSum(vector<int>& nums, int k, vector<vector<int>>& edges) {
        long long totalMaxSum = 0; // 用於儲存節點的累積最大和的變數。
        long long minFlipDifference = LLONG_MAX; // 跟踪最小的翻轉差。
        long long flipCount = 0; // 計算有益的翻轉次數的計數器。
        long long numNodes = nums.size(); // 樹中節點的總數。
        
        for (int i = 0; i < numNodes; i++) {
            long long originalValue = nums[i]; // 節點的原始值。
            long long flippedValue = nums[i] ^ k; // 節點值與 k 進行 XOR 後的值。
            
            // 將原始值或翻轉值的最大值加到總最大和中。
            totalMaxSum += max(originalValue, flippedValue);
            
            // 更新最小翻轉差。
            minFlipDifference = minValue(minFlipDifference, abs(originalValue - flippedValue));
            
            // 基於 XOR 的翻轉計數器，以確定翻轉是否有益。
            flipCount ^= flippedValue > originalValue;
        }
        
        // 根據翻轉計數和最小翻轉差調整總最大和。
        return totalMaxSum - minFlipDifference * flipCount;
    }
};

Python

class Solution:
    # 函數返回兩個長整數中的最小值。
    def minValue(self, a, b):
        return a if a < b else b

    # 函數計算通過翻轉邊得到的值的最大可能總和。
    def maximumValueSum(self, nums, k, edges):
        totalMaxSum = 0  # 變數儲存節點的累計最大總和。
        minFlipDifference = float('inf')  # 跟蹤最小的翻轉差異。
        flipCount = 0  # 計數來檢查有多少次翻轉是有利的。
        numNodes = len(nums)  # 樹中節點的總數。
        
        for i in range(numNodes):
            originalValue = nums[i]  # 節點的原始值。
            flippedValue = nums[i] ^ k  # 節點在與k做異或運算後的值。
            
            # 將原始值或翻轉值中的最大值加到總最大和中。
            totalMaxSum += max(originalValue, flippedValue)
            
            # 更新最小翻轉差。
            minFlipDifference = self.minValue(minFlipDifference, abs(originalValue - flippedValue))
            
            # 基於異或操作的翻轉計數器來決定翻轉是否有利。
            flipCount ^= flippedValue > originalValue
        
        # 根據翻轉計數和最小翻轉差對總最大和進行調整。
        return totalMaxSum - minFlipDifference * flipCount

複雜度分析

• 時間複雜度: $O(n)$

  該算法的時間複雜度是 $O(n)$，其中 $n$ 是樹中節點的數量（這同時也是 nums 陣列的長度）。這是因為算法通過考慮原始值和 XOR 後的值，對每個節點迭代一次以計算潛在的最大和。迴圈內的操作，包括計算 XOR、確定最大值、更新最小翻轉差異以及更新翻轉計數器，都需要常數時間 $O(1)$。因此，通過所有節點進行一次迭代構成線性時間複雜度。

• 空間複雜度: $O(1)$

  該算法的空間複雜度是 $O(1)$，這意味著無論輸入大小如何，它都需要恆定的額外空間。算法主要使用固定數量的變量：totalMaxSum、minFlipDifference、flipCount 和 numNodes。這些變量儲存計算最大和過程中使用的中間計算值，並不依賴於輸入的大小。因此，空間需求不會隨輸入大小而變化，導致恆定的空間複雜度。