題目資訊

題目編號: 311
題目連結: Sparse Matrix Multiplication
主題: Array, Hash Table, Matrix

題目敘述

給定兩個稀疏矩陣 mat1 大小為 $m \times k$ 和 mat2 大小為 $k \times n$，返回 $mat1 \times mat2$ 的結果。你可以假設計算乘法總是可能的。

範例 1：

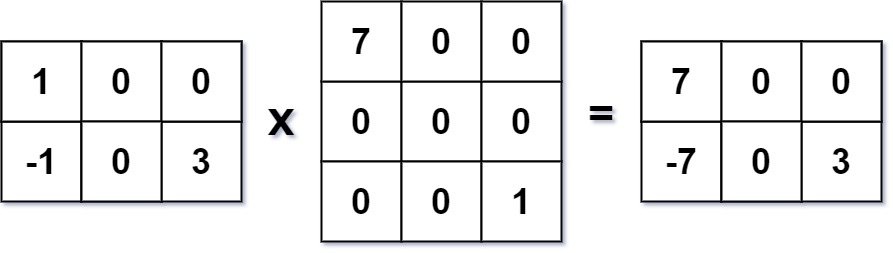
Example 1

輸入：mat1 = [[1,0,0],[-1,0,3]]，mat2 = [[7,0,0],[0,0,0],[0,0,1]]
輸出：[[7,0,0],[-7,0,3]]

範例 2：

輸入：mat1 = [[0]]，mat2 = [[0]]
輸出：[[0]]

約束條件：

$m == \text{mat1.length}$
$k == \text{mat1[i].length} == \text{mat2.length}$
$n == \text{mat2[i].length}$
$1 \leq m, n, k \leq 100$
$-100 \leq \text{mat1[i][j]}, \text{mat2[i][j]} \leq 100$

直覺

在處理兩個稀疏矩陣的乘法時，重要的是要意識到大多數涉及的元素都是零，對最終的乘積沒有任何影響。因此，通過專注於非零元素，可以顯著減少計算工作量。這一見解引導我們採用一種方法，在矩陣乘法過程中跳過零元素，確保只執行必要的計算，並減少不必要的迭代。

解法

為了有效解決將兩個稀疏矩陣（mat1大小為 $m \times k$，mat2大小為 $k \times n$）相乘的問題，我們可以藉助其稀疏性，僅迭代非零元素。該過程可以分解為以下步驟：

結果初始化：創建一個大小為 $m \times n$ 的結果矩陣，並以零初始化。該矩陣將最終儲存 mat1 和 mat2 的乘積。
遍歷 mat1：按照每列 k 進行 mat1 的每一行 i 的迭代。
跳過 mat1 中的零元素：如果元素 mat1[i][k] 是零，則跳到 mat1 的下一列，因為此元素不會對最終乘積產生貢獻。
遍歷 mat2：對於每一個非零元素 mat1[i][k]，迭代 mat2 中的每一列 j。
跳過 mat2 中的零元素：同樣地，如果 mat2[k][j] 是零，則跳到下一列，因為它對結果矩陣沒有貢獻。
計算並累加結果：對於非零元素，計算 mat1[i][k] 和 mat2[k][j] 的乘積，並將其加到 result[i][j] 中。此步驟直接累加結果矩陣中必要的乘積。
返回結果：完成所有相關的迭代後，result 矩陣將包含計算出的 mat1 和 mat2 的乘積，可以作為最終輸出返回。

這種方法有效利用矩陣的稀疏特性，僅執行必要的操作，使矩陣乘法過程比可能會迭代計算不必要的以零為基礎的乘積的簡單計算更為高效。

程式碼

C++

class Solution {
public:
    // 函數用於相乘兩個稀疏矩陣mat1和mat2
    vector<vector<int>> multiply(vector<vector<int>>& mat1, vector<vector<int>>& mat2) {
        int rowsMat1 = mat1.size();            // mat1的行數
        int commonDim = mat1[0].size();        // mat1的列數或mat2的行數
        int colsMat2 = mat2[0].size();         // mat2的列數
        
        // 初始化結果矩陣為零矩陣
        vector<vector<int>> result(rowsMat1, vector<int>(colsMat2, 0));
        
        // 逐行逐列遍歷mat1的每個元素
        for (int i = 0; i < rowsMat1; i++) {
            for (int k = 0; k < commonDim; k++) {
                // 跳過mat1中的零元素，因為它們不貢獻結果
                if (mat1[i][k] == 0) continue;
                
                // 逐列遍歷mat2的每個元素
                for (int j = 0; j < colsMat2; j++) {
                    // 跳過mat2中的零元素，因為它們不貢獻結果
                    if (mat2[k][j] == 0) continue;
                    
                    // 累加在結果矩陣相應單元格中的乘積
                    result[i][j] += mat1[i][k] * mat2[k][j];
                }
            }
        }
        
        return result; // 返回計算出的乘積矩陣
    }
};

Python

class Solution:
    # 函數用於將兩個稀疏矩陣 mat1 和 mat2 相乘
    def multiply(self, mat1, mat2):
        rowsMat1 = len(mat1)            # mat1 的行數
        commonDim = len(mat1[0])        # mat1 的列數或 mat2 的行數
        colsMat2 = len(mat2[0])         # mat2 的列數
        
        # 用零初始化結果矩陣
        result = [[0 for _ in range(colsMat2)] for _ in range(rowsMat1)]
        
        # 遍歷 mat1 的每個元素，逐行逐列
        for i in range(rowsMat1):
            for k in range(commonDim):
                # 跳過 mat1 中的零元素，因為它們不會對結果有貢獻
                if mat1[i][k] == 0:
                    continue
                
                # 遍歷 mat2 的每個元素，逐列
                for j in range(colsMat2):
                    # 跳過 mat2 中的零元素，因為它們不會對結果有貢獻
                    if mat2[k][j] == 0:
                        continue
                    
                    # 在結果矩陣的對應位置累加乘積
                    result[i][j] += mat1[i][k] * mat2[k][j]
        
        return result  # 返回運算結果矩陣

複雜度分析

時間複雜度: $O(m \times k \times n)$
該演算法的時間複雜度為 $O(m \times k \times n)$，其中 $m$ 是 mat1 的行數，$k$ 是 mat1 的列數（或等價於 mat2 的行數），$n$ 是 mat2 的列數。這是因為該演算法會遍歷 mat1 的每一個元素，並且對於每個非零元素，會遍歷 mat2 的相應行。儘管由於矩陣的稀疏性（跳過零元素）可能會有性能提升，在最壞情況下，仍然需要訪問每個元素，因此時間複雜度如上所述。
空間複雜度: $O(m \times n)$
空間複雜度為 $O(m \times n)$，因為為了存儲 mat1 和 mat2 的乘積，需要初始化一個大小為 $m \times n$ 的結果矩陣。沒有使用其他顯著影響空間複雜度的數據結構，因此所需的空間僅由結果矩陣的大小決定。

CS Note
En

Leetcode 311. Sparse Matrix Multiplication

題目資訊

題目敘述

直覺

解法

程式碼

C++

Python

複雜度分析