Leetcode 317. Shortest Distance from All Buildings

Jimmy   Apr 7, 2025   617 words   ~15 mins
#Array #Breadth-First Search #Matrix

Table of Contents

題目資訊

題目敘述

你有一個 $m \times n$ 的網格 grid，其值為 0、1 或 2，其中：

  • 每個 0 代表一片可以自由通過的空地，
  • 每個 1 代表一座不能穿過的建築，
  • 每個 2 代表一個不能穿過的障礙。

你希望在一片空地上建造一間房子，該房子能以最短的總旅行距離到達所有建築。你只能向上、向下、向左和向右移動。

返回這樣一間房子的最短旅行距離。如果按照上述規則無法建造這樣的房子，則返回 -1。

總旅行距離是朋友的房子與會合點之間的距離之和。

範例 1: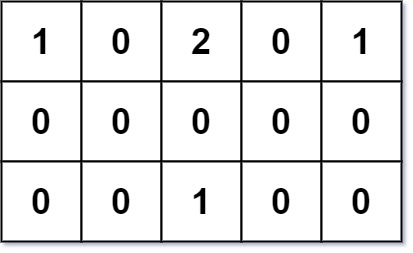
範例 1 圖片

  • 輸入: grid = [[1,0,2,0,1],[0,0,0,0,0],[0,0,1,0,0]]
  • 輸出: 7
  • 解釋: 給定三個建築在 $(0,0)$, $(0,4)$, $(2,2)$，以及一個障礙在 $(0,2)$。點 $(1,2)$ 是建造房子的理想空地，因為總旅行距離 $3+3+1=7$ 是最小的。因此返回 7。

範例 2:

  • 輸入: grid = [[1,0]]
  • 輸出: 1

範例 3:

  • 輸入: grid = [[1]]
  • 輸出: -1

約束條件:

  • $m == \text{grid.length}$
  • $n == \text{grid[i].length}$
  • $1 \le m, n \le 50$
  • grid[i][j] 的值是 0、1 或 2。
  • 網格中至少有一座建築。

直覺

此問題要求在網格上找到一個合適的空地，以便在那裡建造房屋，使得到所有現有建築物的旅行距離最小化。由於移動方向僅限於向上、向下、向左和向右，因此廣度優先搜索（BFS）是探索網格上最短路徑的自然選擇。每個建築物作為BFS的源頭，有效地計算到所有其他可到達點的最短距離，同時從所有建築物累積這些距離。目標是找出不僅可從所有建築物到達，還能使總旅行距離最小化的空地。

解法

此解法包含若干步驟。我們可以按以下部分來分解該演算法的實施：

  1. 初始化：

    • 首先確定網格的大小，m x n，並初始化各種輔助結構。具體而言，準備兩個二維矩陣，building_count和distance，分別用於計算每個空地可以到達多少建築物，以及累積到每個可用單元格的旅行距離。
    • 一個數組moves用於在BFS遍歷期間促進方向性運動。

  2. 廣度優先搜索（BFS）遍歷：

    • 遍歷網格中的每個單元格以識別建築物（grid[i][j] == 1）。對於每個建築，啟動BFS，深入探索所有可達的空地並適當更新building_count和distance矩陣。
    • BFS使用隊列追踪位置和當前的累計距離。每個可達的相鄰空地單元格被標記，遍歷狀態逐漸更新以涵蓋距離和可達性。
    • 在遍歷過程中，確保索引合法、未訪問狀態，並確認目的單元格是空地（grid[next_y][next_x] == 0）。每個合法的、可達的單元格依據累計距離及可達性進行更新。

  3. 決定最佳空地：

    • 隨著對所有建築物的BFS完成，檢查building_count矩陣，以找到可從所有建築物到達的空地（building_count[i][j] == total_building_count）。
    • 使用變量answer來追蹤這些有效單元格中所累積旅行距離的最小值，並僅在找到更低值時進行更新。

  4. 返回結果：

    • 如果找到了任何適合建造房屋且使總旅行距離最小化的空地，則返回此值。如果無法從所有建築物可行地到達任何此類空地，則函數輸出-1，表示在給定限制下的不可能性。

通過從每個建築物進行的系統性BFS，該演算法有效地計算並比較到潛在房屋位置的路徑距離，確保根據問題要求選擇最佳選擇。

程式碼

C++

class Solution {
public:
    int shortestDistance(vector<vector<int>>& grid) {
        int m = grid.size(); // 格子的行數
        int n = grid[0].size(); // 格子的列數
        int total_building_count = 0; // 格子中建築物的總數量

        // 在格子中移動的方向：右、下、左、上
        int moves[] = {1, 0, -1, 0, 1}; 

        // 用來跟蹤從每個空地單元格可達的建築物數量
        vector<vector<int>> building_count(m, vector<int>(n, 0));
        // 用來累積從所有建築物到每個空地單元格的距離
        vector<vector<int>> distance(m, vector<int>(n, 0));

        // 遍歷格子以找到建築物並從每個建築物執行BFS
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (grid[i][j] == 1) {
                    total_building_count++;

                    // 在BFS期間追蹤已訪問過的單元格
                    vector<vector<bool>> visited(m, vector<bool>(n, false));
                    // 使用一個隊列進行BFS；每個元素是一對座標和當前的距離
                    queue<pair<pair<int, int>, int>> bfs;
                    bfs.push({{i, j}, 0});

                    while (!bfs.empty()) {
                        auto [pos, cur_dist] = bfs.front(); // 獲取隊列的頭元素
                        auto& [cur_y, cur_x] = pos; // 當前座標
                        bfs.pop();

                        // 探索所有4個可能的移動（右、下、左、上）
                        for (int k = 0; k < 4; k++) {
                            int next_y = cur_y + moves[k];
                            int next_x = cur_x + moves[k + 1];

                            // 檢查座標是否有效，是否未訪問過，並且是否可作為空地通過
                            if (next_y < 0 || next_y >= m || next_x < 0 || next_x >= n || 
                                visited[next_y][next_x] || grid[next_y][next_x] != 0) {
                                continue;
                            }

                            // 標記此單元格為已訪問
                            visited[next_y][next_x] = true;
                            // 在這一步中增加一單位的距離
                            distance[next_y][next_x] += cur_dist + 1;
                            // 增加可達建築物計數
                            building_count[next_y][next_x]++;
                            // 將新位置和更新的距離推入隊列
                            bfs.push({{next_y, next_x}, cur_dist + 1});
                        }
                    }
                }
            }
        }

        int answer = -1; // 用來保存最小距離的變數

        // 遍歷格子以找到建房的最佳空地
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                // 僅考慮那些可以從所有建築物到達的空地
                if (grid[i][j] == 0 && building_count[i][j] == total_building_count) {
                    if (answer == -1 || answer > distance[i][j]) {
                        answer = distance[i][j]; // 更新最短距離
                    }
                }
            }
        }

        return answer; // 返回最短總旅程距離
    }
};

Python

from collections import deque

class Solution:
    def shortestDistance(self, grid):
        m = len(grid)  # 網格的行數
        n = len(grid[0])  # 網格的列數
        total_building_count = 0  # 網格中建築物的總數

        # 在網格中移動的方向：右，下，左，上
        moves = [1, 0, -1, 0, 1]

        # 用於跟蹤從每個空地單元格可到達的建築物
        building_count = [[0] * n for _ in range(m)]
        # 用於累積從所有建築物到每個空地單元格的距離
        distance = [[0] * n for _ in range(m)]

        # 遍歷網格以找到建築物並從每個建築物進行廣度優先搜索（BFS）
        for i in range(m):
            for j in range(n):
                if grid[i][j] == 1:
                    total_building_count += 1
                    # 在BFS過程中跟踪已訪問的單元格
                    visited = [[False] * n for _ in range(m)]
                    # 使用佇列進行BFS；每個元素是座標對以及當前距離
                    bfs = deque()
                    bfs.append(((i, j), 0))

                    while bfs:
                        (cur_y, cur_x), cur_dist = bfs.popleft()

                        # 探索所有4個可能的移動方向（右，下，左，上）
                        for k in range(4):
                            next_y = cur_y + moves[k]
                            next_x = cur_x + moves[k + 1]

                            # 檢查有效座標、未訪問狀態及作為空地的可通行性
                            if (0 <= next_y < m and 0 <= next_x < n and
                                    not visited[next_y][next_x] and grid[next_y][next_x] == 0):
                                # 標記此單元格為已訪問
                                visited[next_y][next_x] = True
                                # 將距離增加1作為此步驟
                                distance[next_y][next_x] += cur_dist + 1
                                # 增加可到達的建築物數量
                                building_count[next_y][next_x] += 1
                                # 將新的位置和更新的距離放入佇列
                                bfs.append(((next_y, next_x), cur_dist + 1))

        answer = -1  # 用來保存最短距離的變數

        # 遍歷網格以找到建築房屋的最佳土地
        for i in range(m):
            for j in range(n):
                # 只考慮可以從所有建築物到達的空地
                if grid[i][j] == 0 and building_count[i][j] == total_building_count:
                    if answer == -1 or answer > distance[i][j]:
                        answer = distance[i][j]  # 更新最短距離

        return answer  # 返回最短的總旅行距離

複雜度分析

  • 時間複雜度: 解法的時間複雜度為 $O(m \times n \times k)$，其中 $m$ 和 $n$ 是網格的維度，$k$ 是網格中的建築物數量。對於每個建築物，利用廣度優先搜索 (Breadth-First Search, BFS) 遍歷整個網格，這需要 $O(m \times n)$ 的時間，從而導致總體複雜度為 $O(m \times n \times k)$。

  • 空間複雜度: 空間複雜度為 $O(m \times n)$。這是由於 building_count、distance 和 visited 矩陣，各佔用 $O(m \times n)$ 的空間。在最壞情況下，BFS 隊列的大小也可以增長到 $O(m \times n)$。

Disclaimer: All reference materials on this website are sourced from the internet and are intended for learning purposes only. If you believe any content infringes upon your rights, please contact me at csnote.cc@gmail.com, and I will remove the relevant content promptly.


Feedback Welcome: If you notice any errors or areas for improvement in the articles, I warmly welcome your feedback and corrections. Your input will help this blog provide better learning resources. This is an ongoing process of learning and improvement, and your suggestions are valuable to me. You can reach me at csnote.cc@gmail.com.