題目資訊

題目編號: 323
題目連結: Number of Connected Components in an Undirected Graph
主題: Depth-First Search, Breadth-First Search, Union Find, Graph

題目敘述

你有一個包含 n 個節點的圖。給定一個整數 n 和一個數組 edges，其中 edges[i] = [a_i, b_i] 表示圖中在 a_i 和 b_i 之間有一條邊。

返回 圖中的連通分量數量。

範例 1:

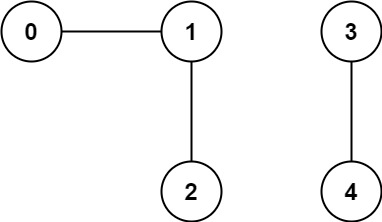
輸入: n = 5, edges = [[0,1],[1,2],[3,4]]
輸出: 2

範例 2:

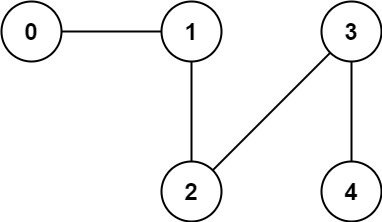
輸入: n = 5, edges = [[0,1],[1,2],[2,3],[3,4]]
輸出: 1

限制條件:

$1 \leq n \leq 2000$
$1 \leq \text{edges.length} \leq 5000$
$\text{edges}[i].\text{length} == 2$
$0 \leq a_i \leq b_i < n$
$a_i \neq b_i$
沒有重複的邊。

直覺

這個問題要求我們確定一個無向圖中連通分量的數量。該圖由 n 個節點和一組給定的邊構成。圖可以被分解為不相交的節點集合，其中每個集合代表一個連通分量。主要的挑戰在於如何有效地識別這些集合。一個有效的方法是使用不相交集聯合集合（Disjoint Set Union, DSU）資料結構，它能夠進行有效的聯合和查找操作，從而使我們能夠在處理每條邊時動態地跟蹤連通分量。

解法

解決方案涉及利用不相交集聯合集合（DSU）資料結構（也稱為並查集）來管理和發現圖中的連通分量。以下是該解法的詳細步驟：

初始化 DSU: 開始時初始化一個大小為 n 的向量 dsu，其中每個節點都是它自己的父節點。這意味着最初每個節點都是一個獨立的連通分量。
查找操作: 實現 findRoot 函數來確定一個節點的根代表元。這涉及沿著父鏈向上遍歷，直到一個節點的父節點是其自身。在這個遍歷過程中，透過將每個節點直接指向根來應用路徑壓縮，這優化了未來的操作。
合併操作: 創建一個 uniteComponents 函數來連接兩個節點 index1 和 index2，藉由將其中一個節點的根連接到另一個節點的根。此操作在節點的根不同時有效地將兩個不相交集合合併為一個集合。
合併邊: 對於輸入中的每條邊，應用 uniteComponents 函數以聯合集合中的節點。這將遞迴地將節點組成連通分量。
計算分量: 為了確定連通分量的數量，遍歷每個節點並使用 findRoot 函數來識別每個節點的根代表元。將這些根代表元收集到集合 rootSet 中，該集合將自然地存儲唯一元素。
返回結果: rootSet 的大小即圖中連通分量的總數，因為每個唯一的根代表一個獨特的連通分量。

藉由遵循這些步驟，該算法有效地識別和計數無向圖中的連通分量，利用 DSU 結構在聯合和查找操作中提供最優的表現。

程式碼

C++

class Solution {
private:
    vector<int> dsu;  // 不相交集聯合（DSU）用於追蹤連通組件

    // 查找給定索引的組件的根代表。
    int findRoot(int index) {
        if (dsu[index] == index) {
            return index;  // 該節點是其自身的根
        } else {
            // 路徑壓縮，將節點直接指向根
            return dsu[index] = findRoot(dsu[index]);
        }
    }

    // 合併兩個節點，通過連接它們的組件。
    void uniteComponents(int index1, int index2) {
        // 如果組件的根不同，則連接這些根
        if (findRoot(index1) != findRoot(index2)) {
            dsu[findRoot(index2)] = findRoot(index1);
        }
    }

public:
    // 計算圖中連通組件的數量
    int countComponents(int n, vector<vector<int>>& edges) {
        dsu.resize(n);  // 初始化 DSU，每個節點作為其自身的父節點

        // 最初將每個節點設置為其自身的父節點
        for (int i = 0; i < n; i++) {
            dsu[i] = i;
        }

        // 合併由邊連接的節點
        for (vector<int>& edge : edges) {
            uniteComponents(edge[0], edge[1]);
        }

        // 用於追蹤唯一根代表的集合
        set<int> rootSet;
        for (int i = 0; i < n; i++) {
            rootSet.insert(findRoot(i));  // 查找每個節點的根
        }

        // 集合的大小表示連通組件的數量
        return rootSet.size();
    }
};

Python

class Solution:
    def __init__(self):
        self.dsu = []  # 不相交集聯盟（DSU）以追蹤連通組件

    # 尋找給定索引的組件的根代表。
    def findRoot(self, index):
        if self.dsu[index] == index:
            return index  # 該節點是其自身的根
        else:
            # 路徑壓縮，通過將節點直接指向根
            self.dsu[index] = self.findRoot(self.dsu[index])
            return self.dsu[index]

    # 通過連接它們的組件來合併兩個節點。
    def uniteComponents(self, index1, index2):
        # 如果組件的根不同則連接它們
        root1 = self.findRoot(index1)
        root2 = self.findRoot(index2)
        if root1 != root2:
            self.dsu[root2] = root1

    # 計算圖中連通組件的數量
    def countComponents(self, n, edges):
        self.dsu = list(range(n))  # 初始化DSU，將每個節點設為它自己的父節點

        # 初始將每個節點設為其自身的父節點
        for i in range(n):
            self.dsu[i] = i

        # 合併那些由邊連接的節點
        for edge in edges:
            self.uniteComponents(edge[0], edge[1])

        # 集合用於追蹤唯一的根代表
        rootSet = set()
        for i in range(n):
            rootSet.add(self.findRoot(i))  # 尋找每個節點的根

        # 集合的大小即為連通組件的數量
        return len(rootSet)

複雜度分析

時間複雜度: $O(n + m \cdot \alpha(n))$，其中 $n$ 是節點數，$m$ 是邊數。複雜度的產生如下：
- 初始化 DSU 需要 $O(n)$ 的時間，因為每個節點被設為其自身的父節點。
- 對於每條邊，會調用 uniteComponents 函數。在 uniteComponents 中調用的 findRoot 函數具有 $O(\alpha(n))$ 的攤還時間複雜度，其中 $\alpha$ 是反阿克曼函數，這是一個非常緩慢增長且對於所有實際用途來說幾乎是常數的函數。因此，處理所有邊需要 $O(m \cdot \alpha(n))$ 的時間。
- 最後的循環用於查找每個節點的根需要 $O(n \cdot \alpha(n))$ 的時間，但它被前一步驟所佔主導，最終導致整體時間複雜度為 $O(n + m \cdot \alpha(n))$。
空間複雜度: $O(n)$。
- DSU 陣列 dsu 有 $n$ 個元素，對應於 $n$ 個節點，導致 $O(n)$ 的空間使用。
- rootSet 的額外空間，用以保存唯一的根代表，在漸進複雜度方面可以忽略不計，因為它最多可以存儲 $n$ 個元素，也導致 $O(n)$ 的空間使用。

CS Note
En

Leetcode 323. Number of Connected Components in an Undirected Graph

題目資訊

題目敘述

直覺

解法

程式碼

C++

Python

複雜度分析