Gradient-Based Learning Applied to Document Recognition
Table of Contents
論文資訊
- Date: November 1998
- Paper - S3
摘要
使用反向傳播演算法訓練的多層神經網路,是目前成功應用梯度式學習技術的代表。只要設計適當的網路結構,梯度式學習演算法可以建立複雜的決策邊界,用來分類像手寫文字這種高維度資料,且只需要非常少量的資料預處理。本文回顧了不同的手寫文字辨識方法,並以標準的手寫數字資料集進行比較。特別是卷積神經網路(Convolutional Neural Networks),因為能夠有效處理二維圖形的變化,因此表現超越了其他方法。
在實際應用中,文件辨識系統通常包含多個模組,例如欄位擷取、分割、文字辨識與語言建模。本文提出一種新方法,稱為圖轉換網路(Graph Transformer Networks, GTN),讓這些多模組系統可以透過梯度式學習方式進行整體訓練,從而提升整體表現。
本文也介紹了兩個線上手寫辨識系統,並透過實驗說明全局訓練的優點,以及圖轉換網路帶來的彈性。
最後,本文描述了一個用於銀行支票讀取的圖轉換網路系統。該系統結合了卷積神經網路的文字辨識器與全局訓練技術,達到了商業與個人支票辨識上的高準確率,且已被商業化應用,每天能處理數百萬張支票。
引言
近年來,機器學習技術,特別是應用於神經網路的技術,在模式識別系統的設計中扮演了越來越重要的角色。事實上,可以說學習技術的進步,是近年來持續語音識別、手寫辨識等應用成功的關鍵因素之一。
本論文的主要觀點是:比起依賴手工設計的啟發式方法,透過自動學習可以建立出更好的模式識別系統。這樣的進展主要得益於機器學習技術與電腦運算能力的發展。以字符識別為例,本研究顯示,過去仰賴人工設計的特徵擷取方法,可以被直接處理像素影像的學習模型所取代。以文件理解為例,過去需要手動整合個別模組的設計方式,可以由一個統一且有理論基礎的方法所取代,這種設計方法稱為圖轉換網路(Graph Transformer Networks, GTN),能夠讓所有模組一起進行訓練,並共同優化整體系統效能。
自從模式識別技術(Pattern recognition)發展以來,由於自然資料(如語音、字元圖形或其他模式)的多樣性與複雜性,使得單靠手工設計很難建立高準確率的識別系統。因此,大多數系統是結合自動學習技術與手工設計方法建構而成。一般而言,辨識單一模式的過程通常包含兩個主要模組,如圖 1 所示。
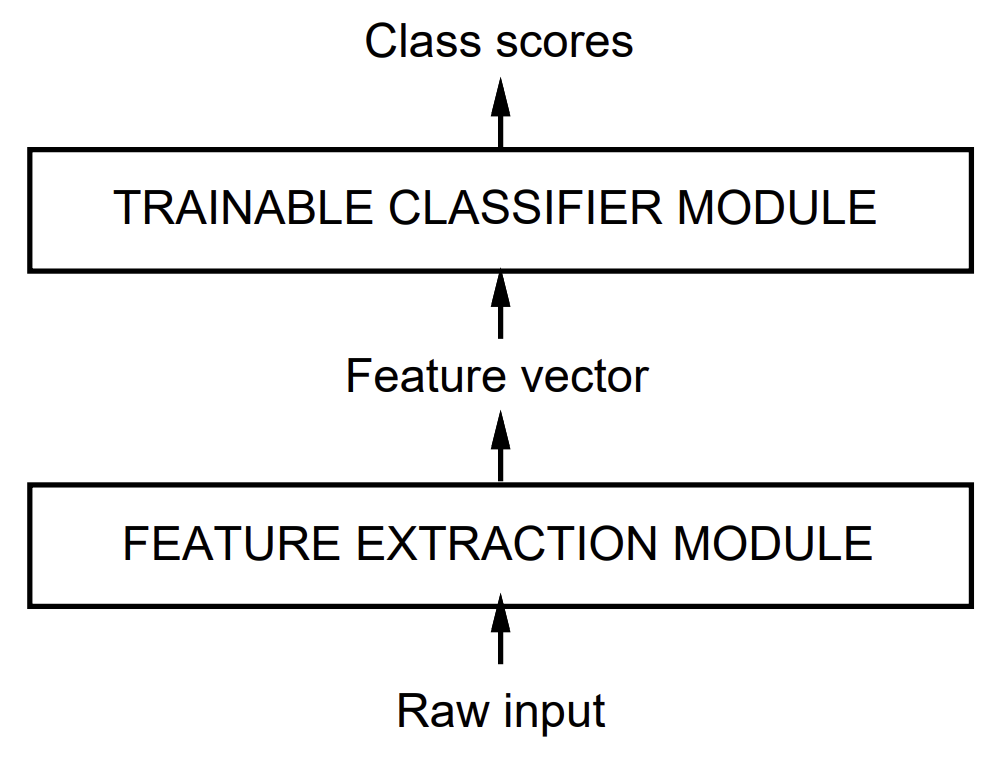
圖 1. 傳統模式識別流程包含兩個模組:固定的特徵擷取器,以及可訓練的分類器。
第一個模組稱為特徵擷取器,負責將輸入的模式轉換成可以用低維向量或符號序列表示的形式。這些表示形式需具備兩個特性:
(a) 可以容易地比對或比較,
(b) 對於不改變輸入本質的轉換與變形具備相對不變性。
特徵擷取器通常包含大量與任務相關的先驗知識,因此設計上相當專門化,也是整個系統設計中最費時費力的部分,並且通常是人工設計完成。
第二個模組是分類器,通常設計為通用且可訓練的模型。然而,這種傳統方法的一大問題在於,整體辨識效果高度依賴於設計者能否定義出合適的特徵。特徵設計是一項困難且需針對每個新問題重新進行的工作。因此,模式識別領域中,有大量研究致力於比較不同特徵集對任務表現的影響。
從資料中學習(Learning from Data)
目前有許多種自動機器學習的方法。其中,近年來最成功的一種方法,是由神經網路領域推廣的「數值型學習」,也叫作基於梯度的學習(gradient-based learning)。
在這種方法中,學習系統會計算一個函數 $Y^p = F(Z^p, W)$。其中,$Z^p$ 是第 $p$ 筆輸入資料,$W$ 則是系統內可調整的參數集合。在圖像分類或模式識別的應用中,$Y^p$ 可以被解讀成資料 $Z^p$ 所屬的類別,或是每個類別的機率分數。系統會使用一個稱為損失函數 $E^p = \mathcal{D}(D^p, F(W, Z^p))$,來衡量目標輸出 $D^p$ 和系統實際輸出結果之間的差異。整體訓練誤差 $E_{\text{train}}(W)$,是所有訓練資料樣本誤差 $E^p$ 的平均值。訓練資料集可以表示為一組已標記的樣本對 ${(Z^1, D^1), …, (Z^P, D^P)}$。最基本的學習目標,就是找到一組參數 $W$,能讓 $E_{\text{train}}(W)$ 盡可能小。
然而,在實際應用中,系統在訓練資料上的表現並不是最重要的。真正重要的是系統在未曾看過的新資料(稱為測試資料)上的表現。通常,會以測試資料集上的錯誤率來評估模型的實用性。許多研究發現,當訓練樣本數量 $P$ 增加時,測試錯誤率 $E_{\text{test}}$ 和訓練錯誤率 $E_{\text{train}}$ 之間的差距會縮小。這個關係可以近似表示為:
$$ E_{\text{test}} - E_{\text{train}} = k \left( \frac{h}{P} \right)^\alpha \tag{1} $$
這裡,$h$ 是機器模型的「有效容量」或複雜度指標,$\alpha$ 是介於 0.5 和 1.0 之間的數值,$k$ 是一個常數。
這個公式說明了兩個重要現象:
- 當訓練資料量 $P$ 增加時,誤差差距會減少。
- 當模型容量 $h$ 增加時,雖然訓練錯誤率 $E_{\text{train}}$ 會下降,但測試誤差可能會上升,因為模型更容易過度擬合訓練資料。
因此,在設計模型時,需要在降低訓練誤差和控制測試誤差之間做出平衡。理想的情況是選擇一個適當的容量 $h$,讓測試錯誤率 $E_{\text{test}}$ 最小化。
大多數學習演算法會同時試圖最小化訓練誤差和誤差差距。
這個目標的正式版本稱為結構風險最小化(Structural Risk Minimization, SRM)。其基本想法是建立一系列模型,這些模型的容量逐漸增加,並對應到參數空間中層層擴展的子集合。
在實作上,結構風險最小化通常透過最小化以下式子來達成:
$$ E_{\text{train}} + \beta H(W) $$
這裡,$H(W)$ 是正則化函數(regularization function),用來對屬於高容量子集的參數 $W$ 賦予較大的值,$\beta$ 是調整兩者權重的常數。
透過最小化 $H(W)$,可以限制模型的複雜度,有效控制過度擬合,同時兼顧訓練誤差與測試誤差的平衡。
實際在開發和訓練機器學習模型時,如果想要達到「結構風險最小化」(Structural Risk Minimization, SRM)這個理論目標,
通常會設定一個新的目標函數,形式如下:
$$ E_{\text{train}}(W) + \beta H(W) $$
這裡每個部分都有重要的意義:
| 項目 | 意義 |
|---|---|
| $E_{\text{train}}(W)$ | 在訓練資料上測量的平均誤差(例如分類錯誤率、均方誤差等等)。這代表「模型對訓練資料的表現」。 |
| $H(W)$ | 正則化(Regularization)函數,用來衡量「參數 $W$ 的複雜度」。例如,可以是 $|W|^2$(參數的平方和)。 |
| $\beta$ | 正則化權重係數,一個常數,用來控制「訓練誤差」與「模型複雜度」這兩者在總目標中的影響比例。 |
這樣設計的原因是什麼?
因為如果你只最小化 $E_{\text{train}}(W)$,模型可能會過度去記住訓練資料,導致「過擬合」(overfitting)問題,雖然在訓練集表現很好,但在新資料上表現很差。
為了解決這個問題,正則化項 $H(W)$ 被引入目標函數中。
它會「懲罰」那些太複雜、太容易過度擬合的模型,讓學習過程中自動偏好「比較簡單的模型」。
換句話說,
👉 你一邊希望模型在訓練集上表現好(小 $E_{\text{train}}(W)$),
👉 但同時又希望模型不要太複雜(小 $H(W)$),
所以兩者加起來成為新的學習目標。
基於梯度的學習(Gradient-Based Learning)
在電腦科學領域,如何根據一組參數去最小化一個函數,一直是個非常核心的問題。
基於梯度的學習(Gradient-Based Learning)就是利用一個重要的事實: “連續、平滑的函數,通常比離散(組合型)函數更容易最小化。”
1. 連續、平滑 ⇒ 可以使用「方向感」來找最低點
- 在連續、平滑的函數裡,每個位置都有一個 斜率(梯度) 可以計算。
- 梯度告訴你:哪個方向可以讓值下降最快。
- 所以你只要一直沿著「下降最快的方向」(負梯度方向)慢慢走,就有機會找到最小值。
簡單講,梯度就像地圖上的指南針,指引你往山谷的方向走。
2. 離散(組合型)函數 ⇒ 沒有平滑斜率,無法用方向感找最低點
- 在離散問題裡,比如選 5 本書組合、排 10 個物品順序,每一種選擇都是分開的。
- 小小改變一點點(比如換一本書、換兩個物品的順序),結果可能差很多,沒有一個「小幅改變 → 小幅變化」的關係。
- 這種情況下,沒有連續的斜率可以告訴你哪裡比較好,只能一個一個試,一直比、一直嘗試(組合爆炸,超級難)。
3. 更數學一點的講法
連續、平滑函數有良好的數學性質,比如:
- 可以用微分描述局部行為
- 可以保證在某些條件下存在局部極小值
- 可以利用許多數學工具(例如泰勒展開、牛頓法)
但離散函數常常是NP-hard問題(超難問題),數量爆炸,無法用梯度技巧處理,只能窮舉或用啟發式方法(像是遺傳演算法、貪婪演算法)。
我們可以透過計算損失函數(Loss Function)在參數發生微小變化時的變化量,來進行最小化。這個變化量就是所謂的梯度(Gradient)。
如果可以 解析式地(數學公式直接) 求出梯度,而不是用試誤法(數值微分)來估算,那麼就能設計出效率很高的學習演算法。
在這篇文章中,假設參數 $W$ 是一個實數向量,而 $E(W)$ 是一個連續且幾乎到處可微分的損失函數。
最簡單的最小化方法就是著名的梯度下降法(Gradient Descent),每次更新參數 $W$ 的方式如下:
$$ W_k = W_{k-1} - \epsilon \frac{\partial E(W)}{\partial W} \tag{2} $$
其中,$\epsilon$ 是一個固定的小常數,叫做學習率(Learning Rate)。
在更複雜的情況下,$\epsilon$ 也可以是隨時間變動的,或者被設計成矩陣、甚至用近似的Hessian矩陣來做更聰明的調整(例如牛頓法或擬牛頓法)。
還有一種叫做 共軛梯度法(Conjugate Gradient Method) 的方法也可以使用。不過,這篇文章的附錄 B 有指出,對於大型學習機器來說,這些複雜的二階方法實際效果很有限。
接著,介紹另一種常見的做法:
一種很受歡迎的最小化方法是隨機梯度下降(Stochastic Gradient Descent, SGD),也叫做線上更新(On-line Update)。
它的做法是:每次只拿一筆資料樣本,計算一次梯度來更新參數,而不是等整個資料集都算完才更新。
數學式如下:
$$ W_k = W_{k-1} - \epsilon \frac{\partial E^{p_k}(W)}{\partial W} \tag{3} $$
這裡的 $E^{p_k}(W)$ 表示的是針對第 $p_k$ 筆樣本計算的損失。
這種做法會讓參數 $W$ 圍繞著一條平均的路徑波動,但通常收斂速度會比傳統梯度下降還要快很多。
尤其是當訓練資料中有很多重複或冗餘資訊時(像是語音辨識、文字辨識),隨機梯度下降會特別有效。
其實,早從 1960 年代起,這類演算法的數學理論就已經被提出,但是真正的成功應用在比較難的任務上,是一直到 1980 年代中期才開始出現。
梯度反向傳播(Gradient Back-Propagation)
自 1950 年代後期開始,梯度式學習(Gradient-Based Learning)方法便被提出並使用,然而當時主要侷限於線性系統的應用。直到後來發生了三個關鍵事件,人們才真正認識到,簡單的梯度下降技巧在複雜機器學習任務中的強大威力。
第一個事件,是發現即使損失函數存在局部最小值,在實際操作中卻並不會對學習造成重大困擾。這一點從早期的非線性梯度學習方法(如 Boltzmann 機器)成功的實驗結果中得到了印證。
第二個事件,是 Rumelhart、Hinton 和 Williams 等人將一種簡單且高效的演算法——反向傳播演算法(Back-Propagation Algorithm) 推廣至大眾。這個方法能夠有效地計算多層非線性系統中每一層的梯度,大幅提升了訓練深度神經網路的可行性。
第三個事件,是證明了將反向傳播應用於多層感知機(Multilayer Neural Networks),尤其是具有 S 型(Sigmoidal)啟動函數的神經元,可以成功解決複雜的學習問題。這進一步確立了反向傳播技術在機器學習領域的核心地位。
反向傳播的基本概念是:
從輸出層開始,逐層向後傳遞誤差信號,並有效率地計算每一層的梯度。
這個想法早在 1960 年代初的控制理論文獻中就被提出,但直到多年後才在機器學習領域獲得重視。
值得一提的是,早期在神經網路學習中的推導方法,並非直接使用梯度下降,而是利用「虛擬目標(Virtual Targets)」或「最小擾動推論(Minimal Disturbance Arguments)」等概念來實現。
後來,控制理論中採用的拉格朗日方法(Lagrange Formalism),為推導反向傳播提供了更嚴謹且一致的方法論,並成功延伸至更複雜的系統,如循環神經網路(RNN)與異質模組網路等。
一個更簡單的多層系統推導方式,則可參考後續章節的介紹。
此外,有一個理論上的有趣現象是:
即便多層神經網路的損失函數中存在局部最小值,實務上卻很少成為困擾。
目前的推測是,當網路結構設計得夠大(這在實際應用中非常常見),參數空間中的「額外維度」可以大幅降低陷入局部極小值的風險。
總體而言,反向傳播技術不僅是目前最普遍使用的神經網路學習方法,更可能是所有形式的學習演算法中應用最廣泛的一種。
真實手寫辨識系統中的學習
辨識單個手寫字元,早就在學術界被大量研究過,並且是神經網路早期成功應用的案例之一。過去的比較實驗也顯示,使用「基於梯度的學習」訓練出來的神經網路,在同樣的資料上表現得比其他方法都更好。其中表現最好的神經網路叫做卷積神經網路(Convolutional Networks),它們可以直接從像素圖像中,自己學會挑選出有用的特徵。
不過,要在真實情境中進行手寫辨識,最困難的地方不只是辨認每一個字元而已,還要能把字元從單詞或句子中切割出來,這個過程叫做切割(Segmentation)。
目前最常見的標準做法叫做啟發式過度切割(Heuristic Over-Segmentation)。這種方法的想法是,先用一些影像處理技術產生出很多可能的切割點,然後再從這些可能的切割中,挑出最適合的組合,讓辨識器去判斷每個候選字元的分數並選出最佳結果。
但這種方式的表現,會受到很多因素影響,比如切割品質好不好、辨識器能不能正確分辨出正確的字元,以及能不能排除被切錯的情況,例如字元破碎、多個字元連在一起,或者其他不正確的切割。
要訓練一個能處理這些問題的辨識器,面臨很大的挑戰,因為要建立一個包含「錯誤切割情形」的標記資料庫很困難。最簡單的方法是,把字串影像跑過切割器後,一個個手動標記所有的候選字元。不過這種做法非常耗時、費工,而且容易標記不一致。舉例來說,一個被切成一半的數字 4,它的右半邊應該標成 1?還是標成非字元?又或者一個數字 8 的右半邊,該標成 3?
為了克服這些問題,研究提出了兩種解法:
第一種解法:整段式訓練,跳過逐字標記
第一個方法,是直接以 整段字串 的層級來訓練系統,而不是單一字元。這樣可以用「基於梯度的學習」來優化整體的結果,讓系統學會最小化整段的錯誤率,而不是每個字單獨訓練。
這樣做有一個好處,就是整個損失函數是可微分的,所以可以順利使用梯度下降等最佳化方法來訓練模型。
此外,研究還提出了 有向無環圖(Directed Acyclic Graphs, DAGs) 的概念,這種圖可以用來表示不同的辨識可能性,並且引出了 圖轉換網路(Graph Transformer Network, GTN) 的想法,幫助模型有效地處理各種可能的輸出結果。
第二種解法:完全不切割,直接掃描辨識
第二個方法更大膽,就是 完全不要做切割 。這種做法是,讓辨識器直接在整張輸入影像上到處掃描,在每個可能的位置上試著辨識字元。
這種方法依靠辨識器的 字元定位能力(Character Spotting) ,也就是辨識器要能夠抓到畫面中正中央出現的單一字元,即使周圍有其他干擾也沒關係,同時也能排除掉那些完全沒有置中字元的圖像。
辨識器在整張圖上掃描後,會產生一連串的輸出結果,接著把這些結果送進 圖轉換網路(GTN) ,這個網路會考慮語言上的限制條件,最後選出最合理的整體解讀。
這個方法跟早期的 隱馬可夫模型(Hidden Markov Models, HMM) 在語音辨識上的做法有點類似。不過,由於現在使用的是卷積神經網路(CNN),所以即使要掃描整張圖,計算量也可以有效降低,讓這種方法在實務上變得非常有吸引力。
全域可訓練系統
如前所述,大多數實用的模式識別系統是由多個模組組成的。例如,一個文件識別系統由以下部分構成:區域定位器(field locator),用來提取感興趣區域;欄位分割器(field segmenter),將輸入影像切割成候選字元的圖像;辨識器(recognizer),用來分類並評分每個候選字元;以及語境後處理器(contextual post-processor),通常基於隨機文法(stochastic grammar),從辨識器生成的假設中選出文法上最正確的答案。
在大多數情況下,模組之間傳遞的資訊最好以帶有數值資訊的圖(graph)來表示,數值資訊附加於連接的弧線(arcs)上。例如,辨識器模組的輸出可以表示為一個無環圖(acyclic graph),其中每條弧線包含一個候選字元的標籤與得分,每條路徑代表輸入字串的一種替代解釋。
通常,每個模組是手動最佳化的,或在脫離上下文的情況下單獨訓練。例如,字元辨識器會以預先切割好的標記字元影像來訓練。然後,將整個系統組裝起來,再手動調整部分模組的參數,以最大化整體效能。這最後的步驟極為繁瑣、耗時,且幾乎可以確定是次優的。
一個更好的替代方法是:嘗試訓練整個系統,以最小化一個全球性誤差指標,例如在文件層級的字元誤分類機率。理想情況下,我們希望找到一個方法,對整個系統的所有參數,最小化這個全局損失函數。如果這個測量系統效能的損失函數 $E$ 可以對系統的可調參數 $W$ 進行微分,那麼就可以利用基於梯度的學習(Gradient-Based Learning),來尋找 $E$ 的局部最小值。
然而,一開始看起來,系統的龐大和複雜似乎會使這件事變得難以實現。
為了確保總損失函數 $E^p(Z^p, W)$ 可微分,整個系統被建構為由可微分模組組成的前饋網路(feed-forward network)。每個模組實現的功能必須是連續且幾乎處處可微的,對其內部參數(例如字元辨識模組中神經網路的權重)及對模組的輸入皆是如此。如果符合這個條件,可以將經典的 反向傳播(back-propagation) 方法做簡單推廣,以有效計算損失函數對系統所有參數的梯度。
例如,考慮一個由許多模組串接而成的系統,每個模組實現一個函數: $$ X_n = F_n(W_n, X_{n-1}) $$ 其中 $X_n$ 是模組的輸出向量,$W_n$ 是該模組的可調參數(是 $W$ 的子集),而 $X_{n-1}$ 是模組的輸入向量(或前一個模組的輸出)。
將輸入 $X_0$ 提供給第一個模組,並生成最終輸出 $Z^p$。
若已知 $E^p$ 對 $X_n$ 的偏導數,則可以用以下反向遞迴公式來計算 $E^p$ 對 $W_n$ 和 $X_{n-1}$ 的偏導數:
$$ \frac{\partial E^p}{\partial W_n} = \frac{\partial F}{\partial W}(W_n, X_{n-1}) \frac{\partial E^p}{\partial X_n} $$ $$ \frac{\partial E^p}{\partial X_{n-1}} = \frac{\partial F}{\partial X}(W_n, X_{n-1}) \frac{\partial E^p}{\partial X_n} \tag{4} $$
其中,$\frac{\partial F}{\partial W}(W_n, X_{n-1})$ 是 $F$ 對 $W$ 的雅可比矩陣(Jacobian),而 $\frac{\partial F}{\partial X}(W_n, X_{n-1})$ 是 $F$ 對 $X$ 的雅可比矩陣。
向量函數的雅可比矩陣是個矩陣,其中包含了所有輸出對所有輸入的偏導數。
第一個公式計算損失函數梯度的一部分,而第二個公式則產生一個反向遞迴,這與神經網路中著名的反向傳播過程一致。
我們可以將訓練樣本的梯度取平均,得到完整的梯度。值得注意的是,在很多情況下,不需要顯式地計算出雅可比矩陣,只需要直接計算偏導數向量的乘積即可,這樣可以更簡單。
與普通的多層神經網路(multi-layer neural networks)類比:除了最後一層以外的所有模組,都叫做隱藏層(hidden layers),因為它們的輸出無法直接從外部觀察。
當系統更複雜時,即使只是單純的模組串接,偏微分的符號表達也會變得很冗長與笨拙。在更一般的情況下,可以使用拉格朗日函數(Lagrangian functions)來推導。
傳統的多層神經網路是一個特例,其中狀態資訊 $X_n$ 是固定維度的向量,模組是經過層層矩陣乘法(權重)和分量級非線性函數(神經元)運算所構成的。
但,如前所述,當處理更複雜的系統時,模組之間傳遞的狀態資訊最好以帶有數值資訊的圖(graph)來表示。在這種情況下,每個模組稱為圖轉換器(Graph Transformer),它們以一個或多個圖作為輸入,並產生圖作為輸出。由此組成的網路稱為圖轉換器網路(Graph Transformer Networks,GTN)。
本論文後續在第四、六和八章節會發展GTN的概念,並說明如何用基於梯度的學習(Gradient-Based Learning),來訓練所有模組的所有參數,以最小化全局損失函數。
儘管看起來似乎矛盾,因為圖這樣的離散物件要怎麼計算梯度,但這個問題可以被克服,後文會進一步說明。
Disclaimer: All reference materials on this website are sourced from the internet and are intended for learning purposes only. If you believe any content infringes upon your rights, please contact me at csnote.cc@gmail.com, and I will remove the relevant content promptly.
Feedback Welcome: If you notice any errors or areas for improvement in the articles, I warmly welcome your feedback and corrections. Your input will help this blog provide better learning resources. This is an ongoing process of learning and improvement, and your suggestions are valuable to me. You can reach me at csnote.cc@gmail.com.