圖解 ROC 曲線與 AUC 概念
Table of Contents
ROC 曲線與 AUC(Area Under the Curve)是什麼?為什麼重要?
在機器學習的二元分類問題中,模型通常會輸出一個「預測分數」表示為正類的機率。例如:一筆交易被判斷為詐騙的機率是 0.9。這時候我們必須設定一個「分類閾值(threshold)」,來決定多少分數以上就算是詐騙。
不同的閾值會影響模型的預測結果,因此我們需要一種方法來全面觀察不同閾值下的模型表現,這正是 ROC 曲線(Receiver Operating Characteristic Curve)與 AUC(Area Under the Curve)所提供的功能。
ROC 曲線(Receiver Operating Characteristic Curve)
為什麼需要 ROC 曲線?
假設我們有一個模型要判斷一筆交易是否為詐騙(正類),模型輸出的是一個機率分數,而不是直接給出分類結果。此時:
- 設定 threshold = 0.8:只有機率高於 0.8 才被判定為詐騙
- 設定 threshold = 0.3:機率超過 0.3 就算詐騙
不同的 threshold,會讓模型預測結果大不相同,甚至影響精確率(Precision)、召回率(Recall)等指標。ROC 曲線便是在所有 threshold 下,觀察模型在「分類能力」上的穩定性與變化。
混淆矩陣是 ROC 曲線的基礎
混淆矩陣(Confusion Matrix)統計了模型的預測與實際之間的差異,包含以下四種結果:
- True Positive(TP):實際為正類,且預測為正類
- False Positive(FP):實際為負類,但預測為正類
- True Negative(TN):實際為負類,且預測為負類
- False Negative(FN):實際為正類,但預測為負類
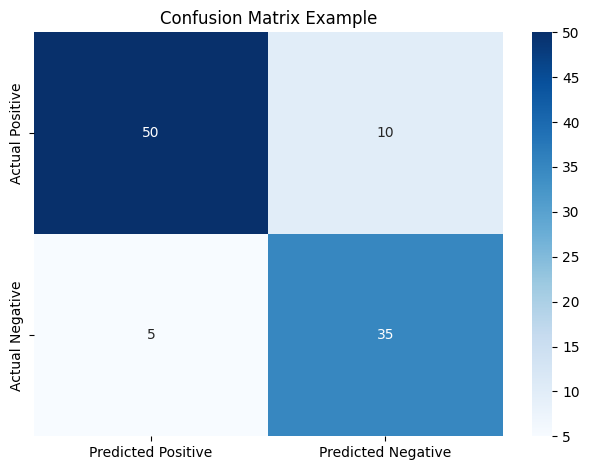
圖 1:混淆矩陣,列表示實際類別,欄表示預測類別。每一格分別對應 TP、FP、TN、FN。
這些數值可用來計算 ROC 曲線中兩個核心指標:
- 真陽性率(True Positive Rate, TPR): $$ \text{TPR} = \frac{TP}{TP + FN} $$
- 假陽性率(False Positive Rate, FPR): $$ \text{FPR} = \frac{FP}{FP + TN} $$
ROC 曲線的繪製方法
ROC 曲線是以 FPR 為 X 軸、TPR 為 Y 軸,描繪不同 threshold 設定下模型表現的曲線。
可以將 threshold 從 1 降到 0,每一個 threshold 都對應一組 (FPR, TPR),連線後就成為一條 ROC 曲線。
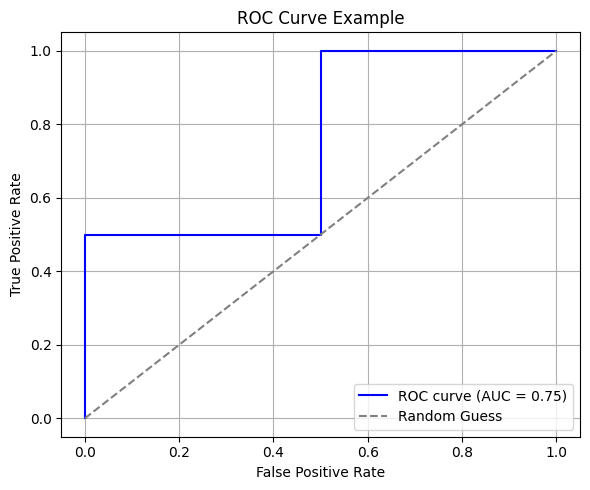
圖 2:ROC 曲線示意圖。虛線表示隨機分類的情況,曲線越靠近左上角表示模型效果越好。
ROC 曲線的意義
- 曲線越接近左上角,模型越能有效區分正負類
- 曲線落在對角線(隨機猜測)附近,表示模型沒有預測能力
- 曲線落在對角線下方,表示模型預測結果與實際相反(若反向使用,可能變成好模型)
AUC(Area Under the Curve)
AUC 的定義
AUC 是 ROC 曲線底下所包圍的面積,數值範圍在 0 到 1 之間。AUC 的意義為:
隨機選取一筆正類資料和一筆負類資料,模型能將正類資料預測分數排在負類之前的機率。
AUC 數值解釋:
| AUC 數值 | 模型表現解釋 |
|---|---|
| 1.0 | 完美分類,完全可分離 |
| 0.8 ~ 0.9 | 良好分類能力 |
| 0.5 | 與隨機猜測相同 |
| < 0.5 | 模型預測結果與實際相反 |
AUC 的圖解理解
AUC 可以用直觀的分數分佈圖來說明。下圖展示模型對正類與負類樣本的分數分佈:
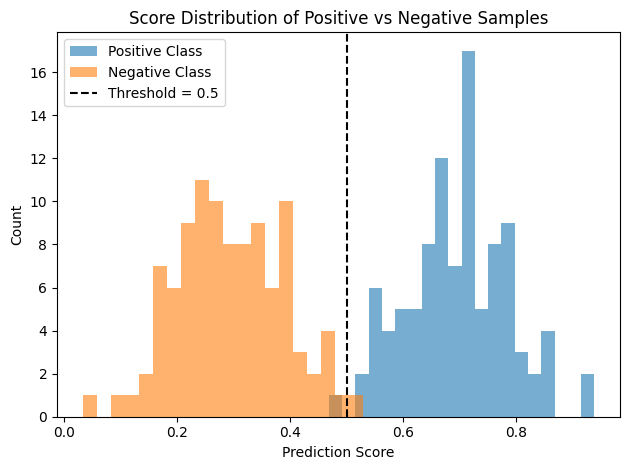
圖 3:正類樣本的預測分數普遍高於負類樣本,代表模型排序能力好,AUC 值高。
為什麼使用 ROC 曲線與 AUC 指標?
ROC 曲線與 AUC 有以下幾個常見的優點:
- 與閾值無關:可以觀察模型在所有可能的 threshold 下的穩定性
- 適合不平衡資料:不受類別比例嚴重不均影響
- 可用來比較不同模型的分類能力
如下圖展示 Logistic Regression 和 Decision Tree 模型的比較結果:
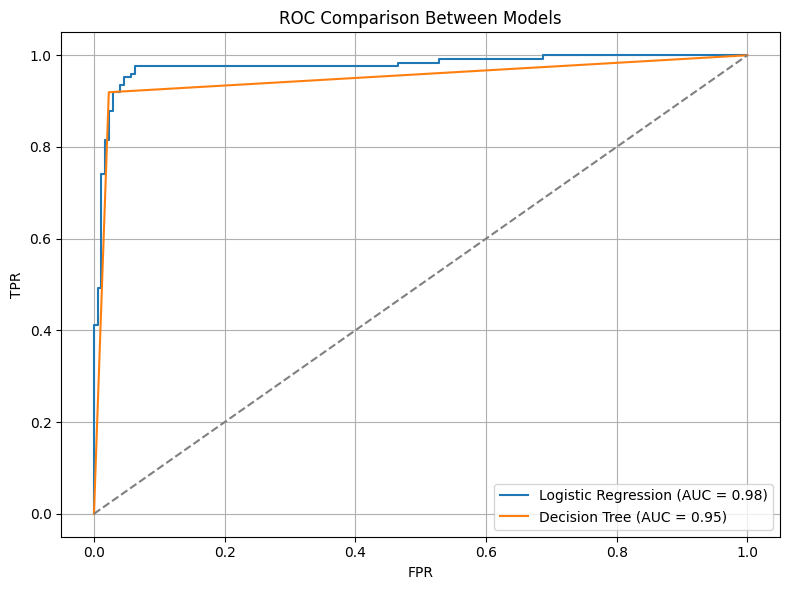
圖 4:兩種模型的 ROC 曲線比較。AUC 越大代表模型分類能力越強。
Python 實作:繪製 ROC 曲線與計算 AUC
以下是用 scikit-learn 實作 ROC 曲線與 AUC 的範例程式碼:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.metrics import roc_curve, auc
# 模擬資料
y_true = np.array([0, 0, 1, 1]) # 實際標籤(0:負類, 1:正類)
y_scores = np.array([0.1, 0.4, 0.35, 0.8]) # 模型預測分數
# 計算 FPR、TPR 與 AUC
fpr, tpr, _ = roc_curve(y_true, y_scores)
roc_auc = auc(fpr, tpr)
# 繪製 ROC 曲線
plt.plot(fpr, tpr, label=f'ROC curve (AUC = {roc_auc:.2f})')
plt.plot([0, 1], [0, 1], linestyle='--', color='gray', label='Random Guess')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC Curve Example')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()
注意事項
- 僅適用於二元分類:若為多分類問題,需進行一對多(One-vs-Rest)轉換
- 忽略機率的準確性:AUC 只考慮分數排序,不代表預測機率是否準確
- 可能誤導實務應用:在實際場景中,高 AUC 並不一定表示商業上有實用價值
總結
ROC 曲線與 AUC 是評估分類模型非常重要的工具,特別是在:
- 模型輸出為機率分數時
- 正負類資料比例不均時
- 想比較多個模型整體分類能力時
建議實務上搭配其他指標(如 Precision-Recall、F1-Score)一併使用,以全面掌握模型表現。
延伸閱讀與參考資料
Disclaimer: All reference materials on this website are sourced from the internet and are intended for learning purposes only. If you believe any content infringes upon your rights, please contact me at csnote.cc@gmail.com, and I will remove the relevant content promptly.
Feedback Welcome: If you notice any errors or areas for improvement in the articles, I warmly welcome your feedback and corrections. Your input will help this blog provide better learning resources. This is an ongoing process of learning and improvement, and your suggestions are valuable to me. You can reach me at csnote.cc@gmail.com.